对于函数 的定义域为D,如果存在区间
的定义域为D,如果存在区间 同时满足下列条件:
同时满足下列条件:
① 在[m,n]是单调的;②当定义域为[m,n]时,
在[m,n]是单调的;②当定义域为[m,n]时,  的值域也是[m,n],则称区间[m,n]是该函数的“H区间”.若函数
的值域也是[m,n],则称区间[m,n]是该函数的“H区间”.若函数 存在“H区间”,则正数
存在“H区间”,则正数 的取值范围是____________.
的取值范围是____________.
我国西部某省4A级风景区内住着一个少数民族村,该村投资了800万元修复和加强民俗文化基础设施,据调查,修复好村民俗文化基础设施后,任何一个月内(每月按30天计算)每天的旅游人数 与第x天近似地满足
与第x天近似地满足 (千人),且参观民俗文化村的游客人均消费
(千人),且参观民俗文化村的游客人均消费 近似地满足
近似地满足 (元).
(元).
(1)求该村的第x天的旅游收入 (单位千元,1≤x≤30,
(单位千元,1≤x≤30, )的函数关系;
)的函数关系;
(2)若以最低日收入的20%作为每一天的计量依据,并以纯收入的5%的税率收回投资成本,试问该村在两年内能否收回全部投资成本?
某厂生产某种产品 (百台),总成本为
(百台),总成本为 (万元),其中固定成本为2万元, 每生产1百台,成本增加1万元,销售收入
(万元),其中固定成本为2万元, 每生产1百台,成本增加1万元,销售收入 (万元),假定该产品产销平衡。
(万元),假定该产品产销平衡。
(1)若要该厂不亏本,产量 应控制在什么范围内?
应控制在什么范围内?
(2)该厂年产多少台时,可使利润最大?
(3)求该厂利润最大时产品的售价。
己知函数f(x)= 在[-1,1]上的最大值为M(a),则函数g(x)=M(x)-
在[-1,1]上的最大值为M(a),则函数g(x)=M(x)- 的零点个数为
的零点个数为
| A.1个 | B.2个 | C.3个 | D.4个 |
已知函数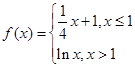 ,则方程
,则方程 恰有两个不同实数根时,实数
恰有两个不同实数根时,实数 的取值范围是( )(注:
的取值范围是( )(注: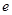 为自然对数的底数)
为自然对数的底数)
A.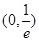 |
B.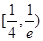 |
C.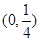 |
D.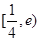 |
已知函数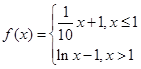 ,则方程
,则方程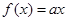 恰有两个不同实数根时,实数
恰有两个不同实数根时,实数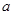 的取值范围是( )(注:
的取值范围是( )(注: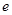 为自然对数的底数)
为自然对数的底数)
A.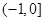 |
B.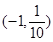 |
C.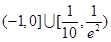 |
D.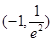 |
已知函数 的定义域为
的定义域为 ,且
,且 的图象连续不间断. 若函数
的图象连续不间断. 若函数 满足:对于给定的
满足:对于给定的 (
( 且
且 ),存在
),存在 ,使得
,使得 ,则称
,则称 具有性质
具有性质 .
.
(Ⅰ)已知函数 ,
, ,判断
,判断 是否具有性质
是否具有性质 ,并说明理由;
,并说明理由;
(Ⅱ)已知函数 若
若 具有性质
具有性质 ,求
,求 的最大值;
的最大值;
(Ⅲ)若函数 的定义域为
的定义域为 ,且
,且 的图象连续不间断,又满足
的图象连续不间断,又满足 ,
,
求证:对任意 且
且 ,函数
,函数 具有性质
具有性质 .
.
设函数 的定义域为
的定义域为 ,若存在闭区间
,若存在闭区间 ,使得函数
,使得函数 满足:①
满足:① 在
在 上是单调函数;②
上是单调函数;② 在
在 上的值域是
上的值域是 ,则称区间
,则称区间 是函数
是函数 的“和谐区间”.下列结论错误的是( )
的“和谐区间”.下列结论错误的是( )
A.函数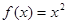 ( (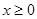 )存在“和谐区间” )存在“和谐区间” |
B.函数 ( (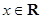 )不存在“和谐区间” )不存在“和谐区间” |
C.函数  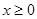 )存在“和谐区间” )存在“和谐区间” |
D.函数 ( (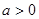 , , )不存在“和谐区间” )不存在“和谐区间” |
已知函数 且函数
且函数 的零点均在区间
的零点均在区间
 内,圆
内,圆 的面积的最小值是( )
的面积的最小值是( )
A. |
B. |
C. |
D. |
对于定义域为 的函数
的函数 ,如果存在区间
,如果存在区间 ,同时满足:
,同时满足:
① 在
在 内是单调函数;②当定义域是
内是单调函数;②当定义域是 ,
, 值域也是
值域也是 ,则称
,则称 是函数
是函数
的“好区间”.
(1)设 (其中
(其中 且
且 ),判断
),判断 是否存在“好区间”,并
是否存在“好区间”,并
说明理由;
(2)已知函数 有“好区间”
有“好区间” ,当
,当 变化时,求
变化时,求 的最大值.
的最大值.