[北京]2013-2014学年北京市海淀区高一上学期期末统考数学试卷
已知函数 ,则下列说法中正确的是( )
,则下列说法中正确的是( )
A.若 ,则 ,则 恒成立 恒成立 |
B.若 恒成立,则 恒成立,则 |
C.若 ,则关于 ,则关于 的方程 的方程 有解 有解 |
D.若关于 的方程 的方程 有解,则 有解,则 |
来源:2013-2014学年北京市海淀区高一上学期期末统考数学试卷
已知函数 ,任取
,任取 ,记函数
,记函数 在区间
在区间 上的最大值为
上的最大值为 最小值为
最小值为 记
记 . 则关于函数
. 则关于函数 有如下结论:
有如下结论:
①函数 为偶函数;
为偶函数;
②函数 的值域为
的值域为 ;
;
③函数 的周期为4;
的周期为4;
④函数 的单调增区间为
的单调增区间为 .
.
其中正确的结论有____________.(填上所有正确的结论序号)
来源:2013-2014学年北京市海淀区高一上学期期末统考数学试卷
已知函数 ,其中
,其中 为常数.
为常数.
(Ⅰ)若函数 在区间
在区间 上单调,求
上单调,求 的取值范围;
的取值范围;
(Ⅱ)若对任意 ,都有
,都有 成立,且函数
成立,且函数 的图象经过点
的图象经过点 ,
,
求 的值.
的值.
来源:2013-2014学年北京市海淀区高一上学期期末统考数学试卷
已知函数 .
.
(Ⅰ)请用“五点法”画出函数 在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);
在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);

(Ⅱ)求函数 的单调递增区间;
的单调递增区间;
(Ⅲ)当 时,求函数
时,求函数 的最大值和最小值及相应的
的最大值和最小值及相应的 的值.
的值.
来源:2013-2014学年北京市海淀区高一上学期期末统考数学试卷
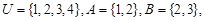 则
则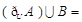 ( )
( )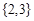
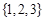


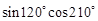 的值为( )
的值为( )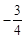

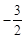
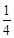
 若
若 共线,则实数
共线,则实数 的值为( )
的值为( )

 或
或
 的定义域为( )
的定义域为( )



 中,
中, 点
点 为
为 中点, 若
中点, 若 ,则
,则 ( )
( )




 的零点所在的区间是( )
的零点所在的区间是( ) )
) )
) )
) )
) 为最小正周期,且在区间
为最小正周期,且在区间 上为减函数的是( )
上为减函数的是( )



 的顶点在坐标原点,始边在
的顶点在坐标原点,始边在 轴的正半轴,终边经过点
轴的正半轴,终边经过点 ,则
,则

 (用“
(用“ ”,“
”,“ ”或“
”或“ ”连接).
”连接). ,则
,则 的值域为 .
的值域为 . 若
若 则
则

 ,则
,则
 ,点
,点 为直线
为直线 上的一个动点.
上的一个动点. 恒为锐角;
恒为锐角; 为菱形,求
为菱形,求 的值.
的值. 的定义域为
的定义域为 ,且
,且 (
( 且
且 ),存在
),存在 ,使得
,使得 ,则称
,则称 .
. ,
, ,判断
,判断 ,并说明理由;
,并说明理由; 若
若 ,
, 且
且 ,函数
,函数 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号