[广东]2014届广东省惠州市高三上学期第二次调研理科数学试卷
“ ”是“直线
”是“直线 :
: 与
与 :
: 平行”的( )
平行”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
来源:2014届广东省惠州市高三上学期第二次调研理科数学试卷
一个几何体的三视图如图所示,其中俯视图与左视图均为半径是 的圆,则这个几何体的体积是 ( )
的圆,则这个几何体的体积是 ( )
A. |
B. |
C. |
D. |
来源:2014届广东省惠州市高三上学期第二次调研理科数学试卷
采用系统抽样方法从 人中抽取
人中抽取 人做问卷调查,为此将他们随机编号为
人做问卷调查,为此将他们随机编号为 ,
, ,……,
,……, ,分组后在第一组采用简单随机抽样的方法抽到的号码为
,分组后在第一组采用简单随机抽样的方法抽到的号码为 .抽到的
.抽到的 人中,编号落入区间
人中,编号落入区间 的人做问卷
的人做问卷 ,编号落入区间
,编号落入区间 的人做问卷
的人做问卷 ,其余的人做问卷
,其余的人做问卷 .则抽到的人中,做问卷
.则抽到的人中,做问卷 的人数为 ( )
的人数为 ( )
A. |
B. |
C. |
D. |
来源:2014届广东省惠州市高三上学期第二次调研理科数学试卷
若盒中装有同一型号的灯泡共 只,其中有
只,其中有 只合格品,
只合格品, 只次品。
只次品。
(1) 某工人师傅有放回地连续从该盒中取灯泡 次,每次取一只灯泡,求
次,每次取一只灯泡,求 次取到次品的概率;
次取到次品的概率;
(2) 某工人师傅用该盒中的灯泡去更换会议室的一只已坏灯泡,每次从中取一灯泡,若是正品则用它更换已坏灯泡,若是次品则将其报废(不再放回原盒中),求成功更换会议室的已坏灯泡所用灯泡只数 的分布列和数学期望.
的分布列和数学期望.
来源:2014届广东省惠州市高三上学期第二次调研理科数学试卷
已知左焦点为 的椭圆过点
的椭圆过点 .过点
.过点 分别作斜率为
分别作斜率为 的椭圆的动弦
的椭圆的动弦 ,设
,设 分别为线段
分别为线段 的中点.
的中点.
(1)求椭圆的标准方程;
(2)若 为线段
为线段 的中点,求
的中点,求 ;
;
(3)若 ,求证直线
,求证直线 恒过定点,并求出定点坐标.
恒过定点,并求出定点坐标.
来源:2014届广东省惠州市高三上学期第二次调研理科数学试卷
 的虚部为( )
的虚部为( ) 



 ,集合
,集合 为函数
为函数 的定义域,则
的定义域,则 ( )
( )



 是等差数列
是等差数列 的前
的前 项和,
项和, ,则
,则 ( )
( )



 应为( )
应为( )




 且函数
且函数 的零点均在区间
的零点均在区间
 内,圆
内,圆 的面积的最小值是( )
的面积的最小值是( )



 则
则 .
. ,则
,则 = .
= . 满足约束条件
满足约束条件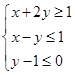 则
则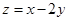 的最大值为 .
的最大值为 . 展开式的常数项是
展开式的常数项是 ,则常数
,则常数 的值为 .
的值为 . 则
则 的值为 .
的值为 . 是曲线
是曲线 上任意一点,则点
上任意一点,则点 的距离的最小值是________.
的距离的最小值是________. 是圆
是圆 的直径
的直径 延长线上一点,
延长线上一点, 是圆
是圆 是切点,
是切点, ,
, ,
, ,
, = .
= .
 .
. 的最小正周期和最值;
的最小正周期和最值; 底面是平行四边形,面
底面是平行四边形,面 面
面 ,
, ,
, ,
, 分别为
分别为 的中点.
的中点.
 ;
;  的余弦值.
的余弦值. 的前
的前 项和是
项和是 ,且
,且 .
. ,求适合方程
,求适合方程 的正整数
的正整数
 时,求函数
时,求函数 在
在 上的极值;
上的极值; 时,
时, ;
;
 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号