若盒中装有同一型号的灯泡共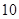 只,其中有
只,其中有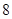 只合格品,
只合格品,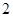 只次品。
只次品。
(1) 某工人师傅有放回地连续从该盒中取灯泡 次,每次取一只灯泡,求
次,每次取一只灯泡,求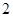 次取到次品的概率;
次取到次品的概率;
(2) 某工人师傅用该盒中的灯泡去更换会议室的一只已坏灯泡,每次从中取一灯泡,若是正品则用它更换已坏灯泡,若是次品则将其报废(不再放回原盒中),求成功更换会议室的已坏灯泡所用灯泡只数 的分布列和数学期望.
的分布列和数学期望.
相关知识点
推荐套卷
若盒中装有同一型号的灯泡共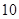 只,其中有
只,其中有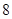 只合格品,
只合格品,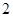 只次品。
只次品。
(1) 某工人师傅有放回地连续从该盒中取灯泡 次,每次取一只灯泡,求
次,每次取一只灯泡,求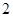 次取到次品的概率;
次取到次品的概率;
(2) 某工人师傅用该盒中的灯泡去更换会议室的一只已坏灯泡,每次从中取一灯泡,若是正品则用它更换已坏灯泡,若是次品则将其报废(不再放回原盒中),求成功更换会议室的已坏灯泡所用灯泡只数 的分布列和数学期望.
的分布列和数学期望.