已知关于x的方程x2+2alog2(x2+2)+a2-3=0有唯一解,则实数a的值为________.
(1)已知α、β是方程x2+(2m-1)x+4-2m=0的两个实根,且α<2<β,求m的取值范围;(2)若方程x2+ax+2=0的两根都小于-1,求a的取值范围.
已知f(x)=2x,g(x)=3-x2,试判断函数y=f(x)-g(x)的零点个数.
设函数f(x)(x∈R)满足f(-x)=f(x),f(x)=f(2-x),且当x∈[0,1]时,f(x)=x3.又函数g(x)=|xcos(πx)|,则函数h(x)=g(x)-f(x)在 上的零点个数为( )
上的零点个数为( )
| A.5 | B.6 | C.7 | D.8 |
若函数y=f(x)(x∈R)满足f(x+1)=f(x-1),且x∈[-1,1]时,f(x)=1-x2,函数g(x)= 则函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数为( )
则函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数为( )
| A.6 | B.7 | C.8 | D.9, |
我们把形如y= (a>0,b>0)的函数因其图象类似于汉字中的“囧”字,故生动地称为“囧函数”,若当a=1,b=1时的“囧函数”与函数y=lg|x|的交点个数为n,则n=________.
(a>0,b>0)的函数因其图象类似于汉字中的“囧”字,故生动地称为“囧函数”,若当a=1,b=1时的“囧函数”与函数y=lg|x|的交点个数为n,则n=________.
若函数y=f(x)(x∈R)满足f(x+1)=-f(x),且x∈[-1,1]时f(x)=1-x2.函数g(x)= 则函数h(x)=f(x)-g(x)在区间[-5,4]内的零点的个数( ).
则函数h(x)=f(x)-g(x)在区间[-5,4]内的零点的个数( ).
| A.7 | B.8, |
| C.9 | D.10 |
已知f(x)是以2为周期的偶函数,当x∈[0,1]时,f(x)= ,那么在区间(-1,3)内,关于x的方程f(x)=kx+k(k∈R)有4个根,则k的取值范围是( ).
,那么在区间(-1,3)内,关于x的方程f(x)=kx+k(k∈R)有4个根,则k的取值范围是( ).
A.0<k≤ 或k= 或k= |
B.0<k≤ |
C.0<k< 或k= 或k= |
D.0<k< |
已知 ,其中
,其中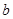 是常数.
是常数.
(1))当 时,
时,  是奇函数;
是奇函数;
(2)当 时,
时, 的图像上不存在两点
的图像上不存在两点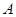 、
、 ,使得直线
,使得直线 平行于
平行于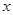 轴.
轴.
已知函数f(x)= ,若函数g(x)=f(x)-k有两个不同的零点,则实数k的取值范围是________.
,若函数g(x)=f(x)-k有两个不同的零点,则实数k的取值范围是________.
直线y=x与函数f(x)= 的图象恰有三个公共点,则实数m的取值范围是 ( ).
的图象恰有三个公共点,则实数m的取值范围是 ( ).
| A.[-1,2) | B.[-1,2] | C.[2,+∞) | D.(-∞,-1] |
若函数 的图像与
的图像与 轴有公共点,则
轴有公共点,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知函数 是偶函数
是偶函数
(1)求k的值;
(2)若函数 的图象与直线
的图象与直线 没有交点,求b的取值范围;
没有交点,求b的取值范围;
(3)设 ,若函数
,若函数 与
与 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数 的取值范围
的取值范围