[上海]2014届上海市高三八校联合调研考试文科数学试卷
已知“ ”是从
”是从 中取出4个元素的一个排列.设
中取出4个元素的一个排列.设 是实数,若“
是实数,若“ ”可推出“
”可推出“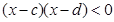 或
或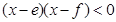 ”,则满足条件的排列“
”,则满足条件的排列“ ”共有_________个.
”共有_________个.
来源:2014届上海市高三八校联合调研考试文科数学试卷
将 的图像向右平移2个单位后得曲线
的图像向右平移2个单位后得曲线 ,将函数
,将函数 的图像向下平移2个单位后得曲线
的图像向下平移2个单位后得曲线 ,
, 与
与 关于
关于 轴对称.若
轴对称.若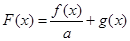 的最小值为
的最小值为 且
且 ,则实数
,则实数 的取值范围为 .
的取值范围为 .
来源:2014届上海市高三八校联合调研考试文科数学试卷
已知公比为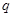 的等比数列
的等比数列 的前
的前 项和为
项和为 ,则下列结论中:
,则下列结论中:
(1) 成等比数列;
成等比数列;
(2) ;
;
(3)
正确的结论为 ( )
| A.(1)(2). | B.(1)(3). | C.(2)(3). | D.(1)(2)(3). |
来源:2014届上海市高三八校联合调研考试文科数学试卷
已知点 、
、 为双曲线
为双曲线 :
: 的左、右焦点,过
的左、右焦点,过 作垂直于
作垂直于 轴的直线,在
轴的直线,在 轴上方交双曲线
轴上方交双曲线 于点
于点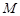 ,且
,且 .圆
.圆 的方程是
的方程是 .
.
(1)求双曲线 的方程;
的方程;
(2)过双曲线 上任意一点
上任意一点 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为 、
、 ,求
,求 的值;
的值;
来源:2014届上海市高三八校联合调研考试文科数学试卷
如图,制图工程师要用两个同中心的边长均为4的正方形合成一个八角形图形.由对称性,图中8个三角形都是全等的三角形,设 .
.
(1)试用 表示
表示 的面积;
的面积;
(2)求八角形所覆盖面积的最大值,并指出此时 的大小.
的大小.
来源:2014届上海市高三八校联合调研考试文科数学试卷
 对应的点到原点的距离为 .
对应的点到原点的距离为 .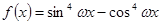
 的最小正周期是
的最小正周期是 ,则
,则 .
. 在向量
在向量 方向上的投影为 .
方向上的投影为 . 过椭圆
过椭圆 的左焦点
的左焦点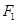 和一个顶点
和一个顶点 ,则椭圆的方程为 .
,则椭圆的方程为 . 的法向量为
的法向量为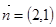 ,则该直线的倾斜角为 .(用反三角函数值表示)
,则该直线的倾斜角为 .(用反三角函数值表示)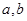 满足
满足 ,则行列式
,则行列式 的最小值为 .
的最小值为 .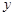 在区间
在区间 内,则输入的实数
内,则输入的实数 的取值范围是 .
的取值范围是 .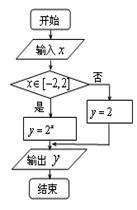
 是一元二次方程
是一元二次方程 的两个虚根.若
的两个虚根.若 ,则实数
,则实数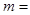 .
. 中,
中, 所对边分别为
所对边分别为 、
、 、
、 .若
.若 ,则
,则 .
. 的首项
的首项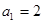 ,其前n项和为
,其前n项和为 .若
.若 ,则
,则 .
. 纬线长度为
纬线长度为 cm,该地球仪的表面积为 cm2.
cm,该地球仪的表面积为 cm2. 与抛物线
与抛物线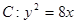 相交于
相交于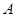 、
、 两点,
两点, 为抛物线
为抛物线 的焦点.若
的焦点.若 ,则实数
,则实数 .
.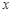 的不等式
的不等式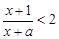 的解集为
的解集为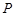 . 若
. 若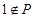 ,则实数
,则实数 的取值范围为 ( )
的取值范围为 ( )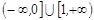 .
.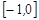 .
. .
. .
. 的反函数是( )
的反函数是( ) .
. .
. .
. .
. 、
、 、
、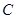 是单位圆上三个互不相同的点.若
是单位圆上三个互不相同的点.若 ,则
,则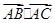 的最小值是( )
的最小值是( ) .
. .
. .
. .
. 中,
中, ,
, ,求:
,求:
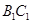 与
与 所成角的大小;
所成角的大小;  的体积.
的体积. ,其中
,其中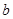 是常数.
是常数. 时,
时,  是奇函数;
是奇函数; 时,
时, 的图像上不存在两点
的图像上不存在两点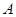 、
、 ,使得直线
,使得直线 平行于
平行于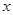 轴.
轴. 和等比数列
和等比数列 中,
中, ,
, ,
, 是
是 项和.
项和.  ,求实数
,求实数 的值;
的值; 中?若存在,求出所有的
中?若存在,求出所有的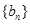 中至少有三项在数列
中至少有三项在数列 中,但
中,但 粤公网安备 44130202000953号
粤公网安备 44130202000953号