高中数学不定方程和方程组试题

设函数，.
（1）解方程：；
（2）令，，求证：

（3）若是实数集上的奇函数，且对任意实数恒成立，求实数的取值范围.

定义在上的函数满足：①当时，②，设关于的函数的零点从小到大依次记为，则________.

已知函数，．
（1）若，求证：函数是上的奇函数；
（2）若函数在区间上没有零点，求实数的取值范围．

设直线l与曲线f（x）=x³+2x+1有三个不同的交点A、B、C，且︱AB︱=︱BC︱=,则直线l的方程为（    ）
A.y=5x+1         B.y=4x+1         C.y=3x+1         D.y=x+1

已知函数，若关于的方程有两个不同的实根，则实数的取值范围是（ ）

A．

B．

C．

D．

方程的正实根个数为（    ）

A．2个

B．3个

C．4个

D．无数个

已知函数，若函数恰有两个不同的零点，则实数的取值范围为      ．

关于方程有唯一的解，则实数的取值范围是________.

已知函数有三个零点，则实数的取值范围为.

对于实数和，定义运算“”：，设，且关于的方程为恰有三个互不相等的实数根，则的取值范围是___________.

已知函数．
（1）当时，判断在的单调性，并用定义证明．
（2）若对任意，不等式 恒成立，求的取值范围；
（3）讨论零点的个数．

给出下列四个命题：
①命题“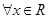，”的否定是“，”；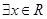
②已知回归直线的斜率的估计值是1.23，样本点的中心为（4，5），则回归直线的方程是；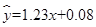
③圆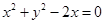的圆心到直线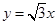的距离是；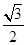
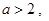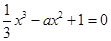④若则方程在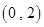上恰好有1个根；
⑤对于大于1的自然数m的二次幂可以用技术进行以下方式的“分裂”：……仿此，若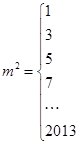，则m=1007；
其中真命题的序号是                 .（填上所有真命题的序号）

给出下列四个命题：
①命题“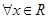，”的否定是“，”；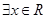
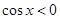②若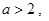则方程在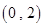上恰好有1个根；
③如果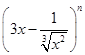的展开式中二项式系数之和为128，则展开式中的系数是；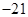
④由直线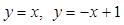，及x轴围成平面图形的面积为；
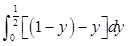其中真命题的序号是                 .（填上所有真命题的序号）

已知函数
（1）求函数的单调区间．
（2）若方程有4个不同的实根，求的范围？
（3）是否存在正数，使得关于的方程有两个不相等的实根？如果存在，求b满足的条件，如果不存在，说明理由．

已知函数，若函数在上有两个零点，则的取值范围是

A．

B．

C．

D．