普通高等学校招生全国统一考试文科数学

设集合$M=\left\{x\left|\right(x+3\left)\right(x-2)<0\right\}$ ，$N=\left\{x|1\le x\le 3\right\}$，则$M\cap N=$（　　）

复数$z=\frac{2-i}{1+i}$（$i$是虚数单位）在复平面内对应的点位于象限为（）

若点$\left(a,9\right)$在函数$y=3^x$的图象上，则$\tan \frac{a\pi }{6}$的值为

曲线$y=x^3+11$在点$P(1,12)$处的切线与$y$轴交点的纵坐标是（）

已知$a,b,c\in R$，命题"若$a+b+c=3$，则$a^2+b^2+c^2\ge 3$"的否命题是（　　）

若函数 $f\left(x\right)=\sin \omega x(\omega >0)$在区间 $[0,\frac{\pi }{3}]$上单调递增，在区间 $[\frac{\pi }{3},\frac{\pi }{2}]$上单调递减，则 $\omega =$（　　）

设变量 $x,y$满足约束条件 $\{\begin{array}{c}x+2y-5\le 0\\ x-y-2\le 0\\ x\ge 0\end{array}$，则目标函数 $z=2x+3y+1$的最大值为（　　）

某产品的广告费用$x$与销售额$y$的统计数据如下表

根据上表可得回归方程$\stackrel{⏜}{y}=\stackrel{⏜}{b}x+\stackrel{⏜}{a}$的$\stackrel{⏜}{b}$为9.4，据此模型预报广告费用为6万元时销售额为（　　）

设$M$$\left(x_0,y_0\right)$为抛物线$C$：$x^2=8y$上一点，$F$为抛物线$C$的焦点，以$F$为圆心、$\left|FM\right|$为半径的圆和抛物线$C$的准线相交，则$y_0$的取值范围是（）

函数 $y=\frac{x}{2}-2\sin x$的图象大致是（　　）

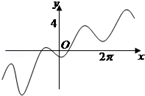
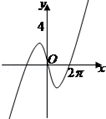
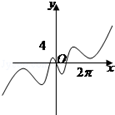
如图是长和宽分别相等的两个矩形．给定下列三个命题：
①存在三棱柱，其正（主）视图、俯视图如图；
②存在四棱柱，其正（主）视图、俯视图如图；
③存在圆柱，其正（主）视图、俯视图如图．
其中真命题的个数是（）

设$A_1,A_2,A_3,A_4$是平面直角坐标系中两两不同的四点，若$\stackrel{\rightharpoonup }{A_1{A}_3}=\lambda \stackrel{\rightharpoonup }{A_1{A}_2}(\lambda \in R)$，$\stackrel{\rightharpoonup }{A_1{A}_4}=\mu \stackrel{\rightharpoonup }{A_1{A}_2}(\mu \in R)$，且$\frac{1}{\lambda }+\frac{1}{\mu }=2$，则称$A_3,A_4$调和分割$A_1,A_2$，已知点$C(c,0)$，$D(d,O)$$(c,d\in R)$调和分割点$A(0,0)$,$B(1,0)$，则下面说法正确的是（）

某高校甲、乙、丙、丁四个专业分别有150、150、400、300名学生，为了解学生的就业倾向，用分层抽样的方法从该校这四个专业共抽取40名学生进行调查，应在丙专业抽取的学生人数为．

执行如图所示的程序框图，输入$l$=2,$m$=3,$n$=5,则输出的$y$的值是．

已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\left(a>0,b>0\right)$和椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为．

已知函数 $f\left(x\right)={\log }_{a}x+x-b$ $\left(a>0,且a\ne 1\right)$.当 $2＜a＜3＜b＜4$时,函数 $f\left(x\right)$的零点 $x_0\in \left(n,n+1\right),n\in N*$,则 $n=$．

在$△ABC$中，内角$A,B,C$的对边分别为$a,b,c$．已知$\frac{\cos A-2\cos C}{\cos B}=\frac{2c-a}{b}$．
（1）求$\frac{\sin C}{\sin A}$的值；
（2）若$\cos B=\frac{1}{4}$$,△ABC$的周长为5，求$b$的长．

甲、乙两校各有3名教师报名支教，期中甲校2男1女，乙校1男2女．
（1）若从甲校和乙校报名的教师中各任选1名，写出所有可能的结果，并求选出的2名教师性别相同的概率；
（2）若从报名的6名教师中任选2名，写出所有可能的结果，并求选出的2名教师来自同一学校的概率．

如图，在四棱台$ABCD-A_1{B}_1{C}_1{D}_1$中，$D_{1}D\perp$平面$ABCD$，底面$ABCD$是平行四边形，$AB=2AD$，$AD=A_1{B}_1$，$\angle BAD=60°$．
（1）证明：$A{A}_1\perp BD$；
（2）证明：$C{C}_1\parallel$平面$A_{1}BD$．

等比数列$\left\{a_n\right\}$中，$a_1,a_2,a_3$分别是下表第一、二、三行中的某一个数，且其中的任何两个数不在下表的同一列．

（1）求数列$\left\{a_n\right\}$的通项公式；
（2）若数列$\left\{b_n\right\}$满足：$b_n=a_n+(-1{)}^n\ln a_n$，求数列$\left\{b_n\right\}$的前$2n$项和$S_{2n}$．

某企业拟建造如图所示的容器（不计厚度，长度单位：米），其中容器的中间为圆柱形，左右两端均为半球形，按照设计要求容器的体积为 $\frac{80\pi }{3}$立方米，且 $1\ge 2r$．假设该容器的建造费用仅与其表面积有关．已知圆柱形部分每平方米建造费用为3千元，半球形部分每平方米建造费用为 $c(c>3)$千元．设该容器的建造费用为 $y$千元．
（1）写出 $y$关于 $r$的函数表达式，并求该函数的定义域；
（2）求该容器的建造费用最小时的 $r$．

在平面直角坐标系$xOy$中，已知椭圆$C:\frac{x^2}{3}+y^2=1$．如图所示，斜率为$k\left(k>0\right)$且不过原点的直线$l$交椭圆$C$于$A$，$B$两点，线段$AB$的中点为$E$，射线$OE$交椭圆$C$于点$G$，交直线$x=-3$于点$D\left(-3,m\right)$．
（1）求$m^2+k^2$的最小值；
（2）若${\left|OG\right|}^2=\left|OD\right|·\left|OE\right|$

（i）求证：直线$l$过定点；
（ii）试问点$B,G$能否关于$x$轴对称？若能，求出此时$△ABG$的外接圆方程；若不能，请说明理由．