山东省青岛市高三4月统一质量检测考试文科数学试卷
在平面直角坐标系中, 为坐标原点,直线
为坐标原点,直线 与圆
与圆 相交于
相交于 两点,
两点, .若点
.若点 在圆
在圆 上,则实数
上,则实数 ( )
( )
A. |
B. |
C. |
D. |
某防疫站对学生进行身体健康调查,欲采用分层抽样的办法抽取样本.某中学共有学生 名,抽取了一个容量为
名,抽取了一个容量为 的样本,已知样本中女生比男生少
的样本,已知样本中女生比男生少 人,则该校共有女生( )
人,则该校共有女生( )
A. 人 人 |
B. 人 人 |
C. 人 人 |
D. 人 人 |
已知三棱锥 中,
中, ,
, ,
, ,
, ,
, ,则关于该三棱锥的下列叙述正确的为( )
,则关于该三棱锥的下列叙述正确的为( )
A.表面积 |
B.表面积为 |
C.体积为 |
D.体积为 |
已知定义在实数集 上的偶函数
上的偶函数 满足
满足 ,且当
,且当 时,
时, ,则关于
,则关于 的方程
的方程 在
在 上根的个数是( )
上根的个数是( )
A. |
B. |
C. |
D. |
已知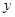 与
与 之间具有很强的线性相关关系,现观测得到
之间具有很强的线性相关关系,现观测得到 的四组观测值并制作了右边的对照表,由表中数据粗略地得到线性回归直线方程为
的四组观测值并制作了右边的对照表,由表中数据粗略地得到线性回归直线方程为 ,其中
,其中 的值没有写上.当
的值没有写上.当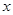 等于
等于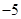 时,预测
时,预测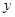 的值为 .
的值为 .
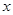 |
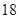 |
 |
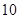 |
 |
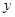 |
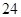 |
 |
 |
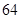 |
对于下列命题:①函数 在区间
在区间 内有零点的充分不必要条件是
内有零点的充分不必要条件是 ;②已知
;②已知 是空间四点,命题甲:
是空间四点,命题甲: 四点不共面,命题乙:直线
四点不共面,命题乙:直线 和
和 不相交,则甲是乙成立的充分不必要条件;③“
不相交,则甲是乙成立的充分不必要条件;③“ ”是“对任意的实数
”是“对任意的实数 ,
, 恒成立”的充要条件;④“
恒成立”的充要条件;④“ ”是“方程
”是“方程 表示双曲线”的充分必要条件.其中所有真命题的序号是 .
表示双曲线”的充分必要条件.其中所有真命题的序号是 .
已知函数 ,
, .
.
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)若函数 图象上的两点
图象上的两点 的横坐标依次为
的横坐标依次为 ,
, 为坐标原点,求
为坐标原点,求 的外接圆的面积.
的外接圆的面积.
已知函数 .
.
(1)从区间 内任取一个实数
内任取一个实数 ,设事件
,设事件 ={函数
={函数 在区间
在区间 上有两个不同的零点},求事件
上有两个不同的零点},求事件 发生的概率;
发生的概率;
(2)若连续掷两次骰子(骰子六个面上标注的点数分别为 )得到的点数分别为
)得到的点数分别为 和
和 ,记事件
,记事件 {
{ 在
在 恒成立},求事件
恒成立},求事件 发生的概率.
发生的概率.
如图,在四棱锥 中,底面
中,底面 为正方形,
为正方形, 平面
平面 ,已知
,已知 ,
, 为线段
为线段 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求四棱锥 的体积.
的体积.
已知函数 ,
, ,其中
,其中 ,
, 为自然对数的底数.
为自然对数的底数.
(1)若 在
在 处的切线
处的切线 与直线
与直线 垂直,求
垂直,求 的值;
的值;
(2)求 在
在 上的最小值;
上的最小值;
(3)试探究能否存在区间 ,使得
,使得 和
和 在区间
在区间 上具有相同的单调性?若能存在,说明区间
上具有相同的单调性?若能存在,说明区间 的特点,并指出
的特点,并指出 和
和 在区间
在区间 上的单调性;若不能存在,请说明理由.
上的单调性;若不能存在,请说明理由.
 ,则
,则 ( )
( )



 ,其中
,其中 为虚数单位,则
为虚数单位,则 的实部为( )
的实部为( )



 为等差数列,
为等差数列, 为等比数列,
为等比数列, ,则
,则 ( )
( )



 (
( )的图象如图所示,则
)的图象如图所示,则 的值为 ( )
的值为 ( ) 




 的值为
的值为 ,则输出
,则输出 的值是( )
的值是( )




 与点
与点 在直线
在直线 的两侧,且
的两侧,且 , 则
, 则 的取值范围是( )
的取值范围是( )



 的焦点坐标为 .
的焦点坐标为 . ,
, 和
和 的夹角为
的夹角为 ,以
,以 为邻边作平行四边形,则该四边形的面积为 .
为邻边作平行四边形,则该四边形的面积为 . 是可导函数,直线
是可导函数,直线 是曲线
是曲线 在
在 处的切线,令
处的切线,令 ,则
,则 .
.
 满足:
满足: 且
且
 .
. ,判断
,判断 是否为等差数列,并求出
是否为等差数列,并求出 ;
; 的前
的前 项的和为
项的和为 ,求
,求 与圆
与圆 相切,且与圆
相切,且与圆 相内切,记圆心
相内切,记圆心 ;设
;设 为曲线
为曲线 轴上的动点,
轴上的动点, 为坐标原点,过点
为坐标原点,过点 作
作 的平行线交曲线
的平行线交曲线 两个不同的点.
两个不同的点. 和
和 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由; 的面积为
的面积为 ,求
,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号