备战高频考点与最新模拟专题3导数与函数
设f(x)是定义在R上的奇函数,当x≤0时,f(x) = 2x2-x,则f(1)=( )
| A.-3 | B.-1 |
| C.1 | D.3 |
(2)设奇函数y=f(x)(x∈R),满足对任意t∈R都有f(t)=f(1-t),且x∈ 时,f(x)=-x2,则f(3)+f
时,f(x)=-x2,则f(3)+f 的值等于________.
的值等于________.
函数f(x)=axm(1-x)n在区间[0,1]上的图象如图所示,则m,n的值可能是( )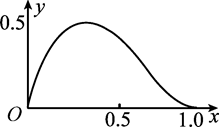
| A.m=1,n=1 | B.m=1,n=2 |
| C.m=2,n=1 | D.m=3,n=1 |
设函数f(x)= 则满足f(x)≤2的x的取值范围是( )
则满足f(x)≤2的x的取值范围是( )
| A.[-1,2] | B.[0,2] | C.[1,+∞) | D.[0,+∞) |
新课标理)若函数f(x)=(1-x2)(x2+ax+b)的图像关于直线x=-2对称,则f(x)的最大值是______.
设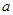 =log36,b=log510,c=log714,则
=log36,b=log510,c=log714,则
| A.c>b>a | B.b>c>a |
| C.a>c>b | D.a>b>c |
陕西理)设[x]表示不大于x的最大整数, 则对任意实数x, y, 有 ( )
| A.[-x] = -[x] | B.[2x] = 2[x] |
| C.[x+y]≤[x]+[y] | D.[x-y]≤[x]-[y] |
福建理)设 是
是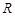 的两个非空子集,如果存在一个从
的两个非空子集,如果存在一个从 到
到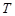 的函数
的函数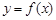 满足:
满足:
 ;
; 对任意
对任意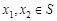 ,当
,当 时,恒有
时,恒有 ,那么称这两个集合“保序同构”,以下集合对不是“保序同构”的是( )
,那么称这两个集合“保序同构”,以下集合对不是“保序同构”的是( )
A.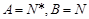 |
B.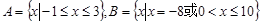 |
C. |
D.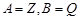 |
北京理)函数f(x)的图象向右平移一个单位长度,所得图象与y=ex关于y轴对称,则f(x)=( )
A. |
B. |
C. |
D. |
福建理)设函数 的定义域为R,
的定义域为R, 是
是 的极大值点,以下结论一定正确的是( )
的极大值点,以下结论一定正确的是( )
A. |
B. 是 是 的极小值点 的极小值点 |
C. 是 是 的极小值点 的极小值点 |
D. 是 是 的极小值点 的极小值点 |
湖南理)设函数
(1)记集合 ,则
,则 所对应的
所对应的 的零点的取值集合为____。
的零点的取值集合为____。
(2)若 .(写出所有正确结论的序号)
.(写出所有正确结论的序号)
①
②
③若
湖南理)已知 ,函数
,函数 。
。
(1)记 求
求 的表达式;
的表达式;
(2)是否存在 ,使函数
,使函数 在区间
在区间 内的图像上存在两点,在该两点处的切线相互垂直?若存在,求
内的图像上存在两点,在该两点处的切线相互垂直?若存在,求 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
上海理)甲厂以x 千克/小时的速度运输生产某种产品(生产条件要求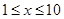 ),每小时可获得利润是
),每小时可获得利润是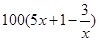 元.
元.
(1)要使生产该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求最大利润.
上海理)给定常数 ,定义函数
,定义函数 ,数列
,数列 满足
满足 .
.
(1)若 ,求
,求 及
及 ;
;
(2)求证:对任意 ,;
,;
(3)是否存在 ,使得
,使得 成等差数列?若存在,求出所有这样的
成等差数列?若存在,求出所有这样的 ,若不存在,说明理由.
,若不存在,说明理由.
天津理)已知函数 .
.
(1) 求函数f(x)的单调区间;
(2) 证明: 对任意的t>0, 存在唯一的s, 使 .
.
(3) 设(2)中所确定的s关于t的函数为 , 证明: 当
, 证明: 当 时, 有
时, 有 .
.
设函数 在R上可导,其导函数为
在R上可导,其导函数为 ,且函数
,且函数 的图像如图所示,则下列结论中一定成立的是
的图像如图所示,则下列结论中一定成立的是
A.函数 有极大值 有极大值 和极小值 和极小值 |
B.函数 有极大值 有极大值 和极小值 和极小值 |
C.函数 有极大值 有极大值 和极小值 和极小值 |
D.函数 有极大值 有极大值 和极小值 和极小值 |
已知函数y=x²-3x+c的图像与x恰有两个公共点,则c=
| A.-2或2 | B.-9或3 | C.-1或1 | D.-3或1 |
“ ”是“函数
”是“函数 在区间
在区间 内单调递增”的( )
内单调递增”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知圆 及以下三个函数:①
及以下三个函数:① ;②
;② ;③
;③ .其中图象能等分圆
.其中图象能等分圆 面积的函数个数为( )
面积的函数个数为( )
| A.3 | B.2 | C.1 | D.0 |
设[x]表示不超过x的最大整数(如[2]=2,[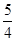 ]=1),对于给定的n
]=1),对于给定的n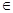 N*,定义
N*,定义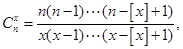 x
x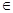
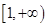 ,则当x
,则当x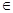
 时,函数
时,函数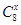 的值域是( )
的值域是( )
A.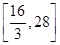 |
B.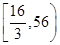 |
C.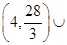 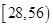 |
D.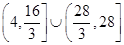 |
关于x的方程ex-1-|kx|=0(其中e=2.71828…是自然对数的底数)的有三个不同实根,则k的取值范围是
| A.{-2,0,2} | B.(1,+∞) | C.{k|k>e} | D.{k|k2>1} |
平面上的点 使关于t的二次方程
使关于t的二次方程 的根都是绝对值不超过1的实数,那么这样的点
的根都是绝对值不超过1的实数,那么这样的点 的集合在平面内的区域的形状是( )
的集合在平面内的区域的形状是( )

对于函数 ,若在定义域存在实数
,若在定义域存在实数 ,满足
,满足 ,则称
,则称 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数 ,试判断
,试判断 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)设 是定义在
是定义在 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围.
的取值范围.
已知函数 ,其中
,其中 ,
, 是自然对数的底数.
是自然对数的底数.
(1)求函数 的零点;
的零点;
(2)若对任意 均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
(3)已知 ,且函数
,且函数 在R上是单调函数,探究函数
在R上是单调函数,探究函数 的单调性.
的单调性.
已知函数
(1)求曲线y=f(x)在(2,f(2))处的切线方程;
(2)若g(x)=f(x)一 有两个不同的极值点.其极小值为M,试比较2M与一3的大小,并说明理由;
有两个不同的极值点.其极小值为M,试比较2M与一3的大小,并说明理由;
(3)设q>p>2,求证:当x∈(p,q)时, .
.
已知函数f(x)=lnx-a2x2+ax(a R).
R).
(l)当a=1时,证明:函数f(x)只有一个零点;
(2)若函数f(x)在区间(1,十 )上是减函数,求实数a的取值范围.
)上是减函数,求实数a的取值范围.
 在[1,2]上的近似解,取中点c=1.5,则下一个有根区间是________.
在[1,2]上的近似解,取中点c=1.5,则下一个有根区间是________. 为正实数,则( )
为正实数,则( )



 的零点个数为( )
的零点个数为( ) ,记
,记 ,已知定义域为
,已知定义域为 的函数
的函数 有反函数
有反函数 ,且
,且 ,若方程
,若方程 有解
有解 ,则
,则
 为实常数,
为实常数, 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, ,若
,若 对一切
对一切 成立,则
成立,则 的定义域为M, 则
的定义域为M, 则 为 ( )
为 ( )

 为奇函数,且当
为奇函数,且当 时,
时, ,则
,则




 设
设 表示
表示 中的较大值,
中的较大值, 表示
表示 得最小值为
得最小值为
 得最小值为
得最小值为 ,则
,则




 的定义域为( )
的定义域为( ) 的图像与函数
的图像与函数 的图像的交点个数为( )
的图像的交点个数为( ) 在
在 是增函数,则a的取值范围是( )
是增函数,则a的取值范围是( )



 ,则函数
,则函数 的定义域( )
的定义域( )


 (x>0)的反函数
(x>0)的反函数 =( )
=( )



 有极值点
有极值点 ,且
,且 ,则关于
,则关于 的方程
的方程 的不同实根个数是
的不同实根个数是 的图像如图所示,在区间
的图像如图所示,在区间 上可找到
上可找到 个不同的数
个不同的数 ,使得
,使得 ,则
,则 的取值范围为
的取值范围为




 (其中
(其中 ).
). 时,求函数
时,求函数 的单调区间;
的单调区间; 时,求函数
时,求函数 上的最大值
上的最大值 .
.
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 的极值
的极值 ,函数
,函数
 在点
在点 处的切线方程;
处的切线方程; 时,求
时,求 的最大值.
的最大值. 在曲线
在曲线 上,点
上,点 在曲线
在曲线 上,则
上,则 最小值为( )
最小值为( )



 ,则( )
,则( ) 为
为 的极大值点
的极大值点 为
为 ,则下列不等式恒成立的是
,则下列不等式恒成立的是



 的图象如图所示,则它与
的图象如图所示,则它与 轴所围图形的面积为
轴所围图形的面积为




 是定义在R上的奇函数,当
是定义在R上的奇函数,当 ,则
,则 = ( )
= ( ) 的单调增区间为( )
的单调增区间为( )



 在区间
在区间 上满足
上满足 ,则满足
,则满足 的
的 的取值范围是
的取值范围是



 的某一切线与直线
的某一切线与直线 平行,则切线方程为 .
平行,则切线方程为 . 若对任意的
若对任意的 ,且
,且

 恒成立,则实数a的取值范围为 .
恒成立,则实数a的取值范围为 . ,则函数
,则函数 的零点个数为 个.
的零点个数为 个. 的图像是中心对称图形,则
的图像是中心对称图形,则 _______.
_______. ,
, 的值域是 .
的值域是 .
 时,求函数
时,求函数 的极值;
的极值; 没有零点,求实数a取值范围.
没有零点,求实数a取值范围. .
. ,
, ,
, ,证明:
,证明: 在区间
在区间 内存在唯一的零点;
内存在唯一的零点; ,若对任意
,若对任意 、
、 ,有
,有 ,求
,求 的取值范围.
的取值范围. .
. 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 时,讨论
时,讨论 的单调性.
的单调性. 是自然对数的底数,函数
是自然对数的底数,函数 。
。 的单调递增区间;
的单调递增区间; 时,函数
时,函数 ,求
,求 的值。
的值。 .
. 时,求函数
时,求函数 单调区间;
单调区间; 在区间[1,2]上的最小值为
在区间[1,2]上的最小值为 ,求
,求 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号