已知函数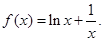
(1)求曲线y=f(x)在(2，f(2))处的切线方程；
(2)若g(x)=f(x)一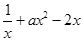
有两个不同的极值点．其极小值为M，试比较2M与一3的大小，并说明理由；
(3)设q>p>2，求证：当x∈(p，q)时，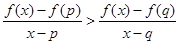
.
相关知识点
推荐套卷
已知函数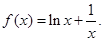
(1)求曲线y=f(x)在(2，f(2))处的切线方程；
(2)若g(x)=f(x)一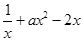有两个不同的极值点．其极小值为M，试比较2M与一3的大小，并说明理由；
(3)设q>p>2，求证：当x∈(p，q)时，.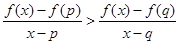
粤公网安备 44130202000953号