普通高等学校招生全国统一考试文科数学
有一个容量为200的样本,其频率分布直方图如图所示,根据样本的频率分布直方图估计,样本数据落在区间[10,12)内的频数为()
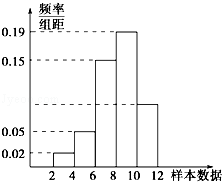
| A. | 18 | B. | 36 | C. | 54 | D. | 72 |
设球的体积为,它的内接正方体的体积为,下列说法中最合适的是
《九章算术》"竹九节"问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第五节的容积为( )
| A. | 1升 | B. |
 升 升
|
C. |
 升 升
|
D. |
 升 升
|
若实数满足,且,则称与互补,记φ那么φ0是与互补的()
| A. | 必要不充分条件 | B. | 充分不必要的条件 |
| C. | 充要条件 | D. | 既不充分也不必要条件 |
某市有大型超市200家、中型超市400家、小型超市1400家.为掌握各类超市的营业情况,现按分层抽样方法抽取一个容量为100的样本,应抽取中型超市家.
在30瓶饮料中,有3瓶已过了保质期.从这30瓶饮料中任取2瓶,则至少取到一瓶已过保质期的概率为.(结果用最简分数表示)
里氏震级
的计算公式为:
,其中
是测震仪记录的地震曲线的最大振幅,是相应的标准地震的振幅,假设在一次地震中,测震仪记录的最大振幅是1000,此时标准地震的振幅
为0.001,则此次地震的震级为
成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列中的.
(Ⅰ)求数列的通项公式;
(Ⅱ)数列的前项和为,求证:数列等比数列.
如图,已知正三棱柱的底面边长为2,侧棱长为,点在侧棱上,点在侧棱上,且,.

(I) 求证:;
(II)求二面角的大小.
提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度(单位:千米/小时)是车流密度(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤≤200时,车流速度是车流密度的一次函数.
(Ⅰ)当0≤≤200时,求函数的表达式;
(Ⅱ)当车流密度为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)可以达到最大,并求出最大值.(精确到1辆/小时).
设函数
,其中
,
为常数,已知曲线
与
在点
处有相同的切线
.
(Ⅰ)求
的值,并写出切线
的方程;
(Ⅱ)若方程
有三个互不相同的实根
,其中
,且对任意的
恒成立,求实数
的取值范围.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号