备战高频考点与最新模拟专题8立体几何

将长方体截去一个四棱锥，得到的几何体如图所示，则该几何体的侧视图为(　　)

如图所示，某几何体的正视图是平行四边形，侧视图和俯视图都是矩形，则该几何体的体积为 (　　)

A．6	B．9
C．12	D．18

一个棱锥的三视图如图，则该棱锥的外接球的表面积为________．

如图，在四面体PABC中，PC⊥AB，PA⊥BC，点D，E，F，G分别是 棱AP，AC，BC，PB的中点．

(1)求证：DE∥平面BCP；
(2)求证：四边形DEFG为矩形；
(3)是否存在点Q，到四面体PABC六条棱的中点的距离相等？说明理由．

如图，在四棱锥P－ABCD中，平面PAD⊥平面ABCD，AB＝AD，∠BAD＝60°，E，F分别是AP，AD的中点．求证：

(1)直线EF∥平面PCD；
(2)平面BEF⊥平面PAD.

如图，平面 PAC⊥平面ABC，△ABC是以AC为斜边的等腰直角三角形，E，F，O分别为 PA，PB，AC的中点，AC＝16，PA＝PC＝10.

(1)设G是OC的中点，证明：FG∥平面BOE；
(2)证明：在△ABO内存在一点M，使FM⊥平面BOE.

·辽宁理）（已知三棱柱

A．

B．

C．

D．

·上海理）如图，在长方体ABCD-A₁B₁C₁D₁中，AB=2,AD=1,A₁A=1，证明直线BC₁平行于平面DA₁C，并求直线BC₁到平面D₁AC的距离.

·广东理）设是两条不同的直线,是两个不同的平面,下列命题中正确的是(    )

A．若,,,则

B．若,,,则

C．若,,,则

D．若,,,则

·大纲理）如图，四棱锥P-ABCD中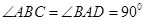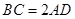，，，和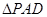都是等边三角形.

（1）证明：；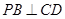
（2）求二面角A-PD-C的大小.

如图，在三棱柱ABC-A₁B₁C₁中，AA₁C₁C是边长为4的正方形.平面ABC⊥平面AA₁C₁C，AB=3，BC=5.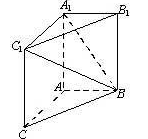

（1）求证：AA₁⊥平面ABC；
（2）求二面角A₁-BC₁-B₁的余弦值；
（3）证明：在线段BC₁存在点D，使得AD⊥A₁B，并求的值.

·北京理）如图，在棱长为2的正方体ABCD-A₁B₁C₁D₁中，E为BC的中点，点P在线段D₁E上，点P到直线CC₁的距离的最小值为          .

·安徽理）如图，正方体的棱长为1，为的中点，为线段上的动点，过点的平面截该正方体所得的截面记为，则下列命题正确的是          （写出所有正确命题的编号）。

①当时，为四边形
②当时，为等腰梯形
③当时，与的交点满足
④当时，为六边形
⑤当时，的面积为

·福建理）如图，在四棱柱中，侧棱底面,


（1）求证：平面
（2）若直线与平面所成角的正弦值为，求的值
（3）现将与四棱柱形状和大小完全相同的两个四棱柱拼成一个新的四棱柱，规定：若拼成的新四棱柱形状和大小完全相同，则视为同一种拼接方案，问共有几种不同的拼接方案？在这些拼接成的新四棱柱中，记其中最小的表面积为，写出的解析式。（直接写出答案，不必说明理由）

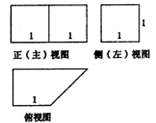
新课标理）某几何函数的三视图如图所示，则该几何的体积为(    )

新课标理）如图，有一个水平放置的透明无盖的正方体容器，容器高8cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm，如果不计容器的厚度，则球的体积为(      )

A．cm3

B．cm3

C．cm3

D．cm3

一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是（1，0，1），（1，1，0），（0，1，1），（0，0，0），画该四面体三视图中的正视图时，以zOx平面为投影面，则得到的正视图可以为

(A)                     (B)                     (C)                  (D)

浙江理）若某几何体的三视图（单位：cm）如图所示，则此几何体的体积等于________。

浙江理）在空间中，过点作平面的垂线，垂足为，记。设是两个不同的平面，对空间任意一点，,恒有，则（  ）

A．平面与平面垂直

B．平面与平面所成的（锐）二面角为

C．平面与平面平行

D．平面与平面所成的（锐）二面角为

陕西理）某几何体的三视图如图所示, 则其体积为        .

辽宁理）（某几何体的三视图如图所示，则该几何体的体积是        .

江西理）如果，正方体的底面与正四面体的底面在同一平面α上，且AB//CD，正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m，n，那么m+n=（    ）

湖南理）已知棱长为1的正方体的俯视图是一个面积为1的正方形，则该正方体的正视图的面积不可能等于（    ）

A．

B．

C．

D．

福建理）已知某一多面体内接于球构成一个简单组合体，如果该组合体的正视图、
俯视图、均如图所示，且图中的四边形是边长为2的正方形，则该球的表面积是_____   

 

三棱柱的侧棱长和底面边长均为，且侧棱底面，其正视图是边长为的正方形，则此三棱柱侧视图的面积为(       )

A．

B．

C．

D．

某几何体的三视图如图所示，则它的表面积为（    ）

A．	B．
C．	D．

某几何体的三视图如图所示，且该几何体的体积是，则正视图中的的值是（ ）

A．2

B．

C．

D． 3

某几何体的三视图如图所示（单位：cm），则该几何体的体积是(    )

A．

B．

C．

D．

一个几何体的三视图如图所示，则该几何体的直观图可以是（    ）

一个几何体的三视图如图所示，则该几何体的表面积为（    ）

A．

B．

C．

D．

已知三棱锥的底面是边长为1的正三角形，其正视图与俯视图如图所示，则其侧视图的面积为（  ）

A．

B．

C．

D．

某几何体的三视图如图所示，则该几何体的体积为（    ）

A．6

B．

C．

D．3

已知某几何体的三视图如图所示，则该几何体的体积为(   )

A．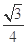

B．

C．

D．

如图是某个四面体的三视图，该四面体的体积为        ．

如图，已知平面四边形中，为的中点，，，
且．将此平面四边形沿折成直二面角，
连接，设中点为．

（1）证明：平面平面；
（2）在线段上是否存在一点，使得平面？若存在，请确定点的位置；若不存在，请说明理由．
（3）求直线与平面所成角的正弦值．

如图,三棱柱中,,,.

(1)证明:;
(2)若,,求三棱柱的体积.

如图，已知四棱锥，底面是等腰梯形，且∥，是中点，平面，， 是中点．

（1）证明：平面平面；（2）求点到平面的距离.

如图，已知四棱锥，底面是等腰梯形，
且∥，是中点，平面，
， 是中点．

（1）证明：平面平面；
（2）求平面与平面所成锐二面角的余弦值.

如图,设是一个高为的四棱锥,底面是边长为的正方形,顶点在底面上的射影是正方形的中心．是棱的中点．试求直线与平面所成角的大小．

如图, 已知四边形ABCD和BCEG均为直角梯形，AD∥BC,CE∥BG，且，平面ABCD⊥平面BCEG，BC=CD=CE=2AD=2BG=2.

（1）求证: EC⊥CD ；
（2）求证：AG∥平面BDE；
（3）求：几何体EG-ABCD的体积.

如图，AB是圆O的直径，点C是弧AB的中点，点V是圆O所在平面外一点，是AC的中点，已知，.

（1）求证：OD//平面VBC；
（2）求证：AC⊥平面VOD；
（3）求棱锥的体积.

如图，在三棱锥中，是等边三角形，.

（1）证明:：；
（2）证明：；
（3）若，且平面平面，求三棱锥体积.

如图1，在直角梯形中，，.把沿折起到的位置，使得点在平面上的正投影恰好落在线段上，如图2所示，点分别为棱的中点.

（1）求证：平面平面；
（2）求证：平面；
（3）若，求四棱锥的体积.

一个空间几何体的三视图如下左图所示，则该几何体的表面积为（   ）

A．48

B．48+8

C．32+8

D．80

如图，在△ABC中，∠ABC=90°，∠A=30。，斜边AC上的中线BD=2，现沿BD将△BCD折起成三棱锥C-ABD，已知G是线段BD的中点，E，F分别是CG，AG的中点．

（1）求证：EF／／平面ABC；
（2）三棱锥C—ABD中，若棱AC=，求三棱锥A一BCD的体积．

如图甲，是边长为6的等边三角形，分别为靠近的三等分点，点为边边的中点，线段交线段于点.将沿翻折，使平面平面，连接，形成如图乙所示的几何体.

（1）求证：平面
（2）求四棱锥的体积.

如图，三棱锥中，，，，点在平面内的射影恰为的重心，M为侧棱上一动点．

（1）求证：平面平面；
（2）当M为的中点时，求直线与平面所成角的正弦值．

如图，四棱锥的底面ABCD是平行四边形，，，面，设为中点，点在线段上且．

（1）求证：平面；
（2）设二面角的大小为，若，求的长．

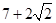
如图，在斜三棱柱中，O是AC的中点，平面，，.

（1）求证：平面；
（2）求二面角的余弦值.

如图所示的多面体中，是菱形，是矩形，面,．

(1)求证：平；
(2)若，求四棱锥的体积．