如图，在△ABC中，∠ABC=90°，∠A=30。，斜边AC上的中线BD=2，现沿BD将△BCD折起成三棱锥C-ABD，已知G是线段BD的中点，E，F分别是CG，AG的中点．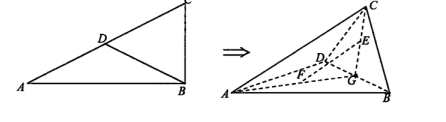
（1）求证：EF／／平面ABC；
（2）三棱锥C—ABD中，若棱AC=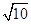
，求三棱锥A一BCD的体积．
在区间
上的平均变化率。
的切线垂直于直线
，试求这条切线的方程。
，过曲线上点
的切线的斜率为
，求
在
处的切线的斜率。
，试计算：（1）在
在
到2，1到
，1到
的平均变
的平均变化率；（3）从以上计算，当
无限增大时，你能得出什么结论？推荐套卷
如图，在△ABC中，∠ABC=90°，∠A=30。，斜边AC上的中线BD=2，现沿BD将△BCD折起成三棱锥C-ABD，已知G是线段BD的中点，E，F分别是CG，AG的中点．
（1）求证：EF／／平面ABC；
（2）三棱锥C—ABD中，若棱AC=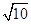，求三棱锥A一BCD的体积．
粤公网安备 44130202000953号