如图, 已知四边形ABCD和BCEG均为直角梯形，AD∥BC,CE∥BG，且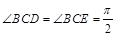
，平面ABCD⊥平面BCEG，BC=CD=CE=2AD=2BG=2.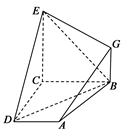
（1）求证: EC⊥CD ；
（2）求证：AG∥平面BDE；
（3）求：几何体EG-ABCD的体积.
推荐套卷
如图, 已知四边形ABCD和BCEG均为直角梯形，AD∥BC,CE∥BG，且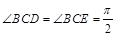，平面ABCD⊥平面BCEG，BC=CD=CE=2AD=2BG=2.
（1）求证: EC⊥CD ；
（2）求证：AG∥平面BDE；
（3）求：几何体EG-ABCD的体积.
粤公网安备 44130202000953号