黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线 恰好落在水平地面和斜坡上,在 处测得电线杆顶端 的仰角为 ,在 处测得电线杆顶端 得仰角为 ,斜坡与地面成 角, ,请你根据这些数据求电线杆的高 .
(结果精确到 ,参考数据: ,

随着人们生活水平的不断提高,旅游已成为人们的一种生活时尚.为开发新的旅游项目,我市对某山区进行调查,发现一瀑布.为测量它的高度,测量人员在瀑布的对面山上 点处测得瀑布顶端 点的仰角是 ,测得瀑布底端 点的俯角是 , 与水平面垂直.又在瀑布下的水平面测得 , (注 、 、 三点在同一直线上, 于点 .斜坡 ,坡角 .求瀑布 的高度.
(参考数据: , , , , , ,
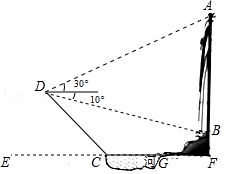
如图,斜坡 ,坡顶 到水平地面的距离 为3米,坡底 为18米,在 处, 处分别测得 顶部点 的仰角为 , ,求 的高度.(结果保留根号)
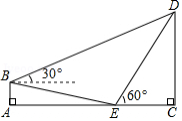
如图, 是一高为4米的平台, 是与 底部相平的一棵树,在平台顶 点测得树顶 点的仰角 ,从平台底部向树的方向水平前进3米到达点 ,在点 处测得树顶 点的仰角 ,求树高 (结果保留根号)

如图,埃航 客机失事后,国家主席亲自发电进行慰问,埃及政府出动了多艘舰船和飞机进行搜救,其中一艘潜艇在海面下500米的 点处测得俯角为 的前下方海底有黑匣子信号发出,继续沿原方向直线航行2000米后到达 点,在 处测得俯角为 的前下方海底有黑匣子信号发出,求海底黑匣子 点距离海面的深度(结果保留根号).

如图,为了测量出楼房 的高度,从距离楼底 处 米的点 (点 与楼底 在同一水平面上)出发,沿斜面坡度为 的斜坡 前进30米到达点 ,在点 处测得楼顶 的仰角为 ,求楼房 的高度(参考数据: , , ,计算结果用根号表示,不取近似值).

某班数学课外活动小组的同学欲测量公园内一棵树 的高度,他们在这棵树正前方一楼亭前的台阶上 点处测得树顶端 的仰角为 ,朝着这棵树的方向走到台阶下的点 处测得树顶端 的仰角为 ,已知 点的高度 为2米,台阶 的坡度 ,且 , , 三点在同一条直线上,请根据以上条件求出树 的高度.(测倾器的高度忽略不计,结果保留根号)

在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动,如图,在测点 处安置测倾器,量出高度 ,测得旗杆顶端 的仰角 ,量出测点 到旗杆底部 的水平距离 ,根据测量数据,求旗杆 的高度.(参考数据: , ,

如图,在一次测量活动中,小丽站在离树底部 处 的 处仰望树顶 ,仰角为 ,已知小丽的眼睛离地面的距离 为 ,那么这棵树大约有多高?(结果精确到 ,参考数据:

如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度 ,求旗杆AB的高度(结果精确到0.1米).参考数据: .

小宇在学习解直角三角形的知识后,萌生了测量他家对面位于同一水平面的楼房高度的想法,他站在自家C处测得对面楼房底端B的俯角为45°,测得对面楼房顶端A的仰角为30°,并量得两栋楼房间的距离为9米,请你用小宇测得的数据求出对面楼房AB的高度.(结果保留到整数,参考数据: )
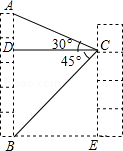
如图所示,某施工队要测量隧道长度 BC, AD=600米, AD⊥ BC,施工队站在点 D处看向 B,测得仰角为45°,再由 D走到 E处测量, DE∥ AC, ED=500米,从点 E看向点 C,测得仰角为53°,求隧道 BC长.(sin53°≈ ,cos53°≈ ,tan53°≈ ).

我市304国道通辽至霍林郭勒段在修建过程中经过一座山峰,如图所示,其中山脚 A、 C两地海拔高度约为1000米,山顶 B处的海拔高度约为1400米,由 B处望山脚 A处的俯角为30°,由 B处望山脚 C处的俯角为45°,若在 A、 C两地间打通一隧道,求隧道最短为多少米(结果取整数,参考数据 ≈1.732)

如图,一座山的一段斜坡 BD的长度为600米,且这段斜坡的坡度 i=1:3(沿斜坡从 B到 D时,其升高的高度与水平前进的距离之比).已知在地面 B处测得山顶 A的仰角为33°,在斜坡 D处测得山顶 A的仰角为45°.求山顶 A到地面 BC的高度 AC是多少米?(结果用含非特殊角的三角函数和根式表示即可)
