初中数学解直角三角形的应用-仰角俯角问题解答题

如图，在办公楼AB和实验楼CD之间有一旗杆EF，从办公楼AB顶部A点处经过旗杆顶部E点恰好看到实验楼CD的底部D点，且俯角为45°，从实验楼CD顶部C点处经过旗杆顶部E点恰好看到办公楼AB的G点，BG＝1米，且俯角为30°，已知旗杆EF＝9米，求办公楼AB的高度．（结果精确到1米，参考数据： $\sqrt{2}\approx 1.41$， $\sqrt{3}\approx 1.73$）

在一次综合实践活动中，小明要测某地一座古塔 AE的高度．如图，已知塔基顶端 B（和 A、 E共线）与地面 C处固定的绳索的长 BC为80 m．她先测得∠ BCA＝35°，然后从 C点沿 AC方向走30 m到达 D点，又测得塔顶 E的仰角为50°，求塔高 AE．（人的高度忽略不计，结果用含非特殊角的三角函数表示）

如图，物理教师为同学们演示单摆运动，单摆左右摆动中，在 OA的位置时俯角∠ EOA＝30°，在 OB的位置时俯角∠ FOB＝60°，若 OC⊥ EF，点 A比点 B高7 cm．求：

（1）单摆的长度（ $\sqrt{3}$ ≈1.7）；

（2）从点 A摆动到点 B经过的路径长（π≈3.1）．

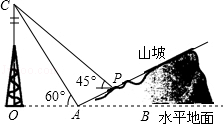
如图所示，某人在山坡坡脚A处测得电视塔尖点C的仰角为60°，沿山坡向上走到P处再测得C的仰角为45°，已知OA＝200米，山坡坡度为 $\frac{1}{3}$（即 $\tan \angle \mathit{PAB}=\frac{1}{3}$），且O，A，B在同一条直线上，求电视塔OC的高度以及此人所在的位置点P的垂直高度．（侧倾器的高度忽略不计，结果保留根号）

某兴趣小组借助无人飞机航拍校园．如图，无人飞机从 A处水平飞行至 B处需8秒，在地面 C处同一方向上分别测得 A处的仰角为75°， B处的仰角为30°．已知无人飞机的飞行速度为4米/秒，求这架无人飞机的飞行高度．（结果保留根号）

如图，某无人机于空中 A处探测到目标 B， D，其俯角分别为30°，60°，此时无人机的飞行高度 AC为60 m，随后无人机从 A处继续飞行30 $\sqrt{3}$ m，到达 A′处，

（1）求 A， B之间的距离；

（2）求从无人机 A′上看目标 D的俯角的正切值．

如图，小明利用学到的数学知识测量大桥主架在水面以上的高度 $\mathit{AB}$ ，在观测点 $C$ 处测得大桥主架顶端 $A$ 的仰角为 $30°$ ，测得大桥主架与水面交汇点 $B$ 的俯角为 $14°$ ，观测点与大桥主架的水平距离 $\mathit{CM}$ 为60米，且 $\mathit{AB}$ 垂直于桥面．（点 $A$ ， $B$ ， $C$ ， $M$ 在同一平面内）

（1）求大桥主架在桥面以上的高度 $\mathit{AM}$ ；（结果保留根号）

（2）求大桥主架在水面以上的高度 $\mathit{AB}$ ．（结果精确到1米）

（参考数据 $\sin 14°\approx 0.24$ ， $\cos 14°\approx 0.97$ ， $\tan 14°\approx 0.25$ ， $\sqrt{3}\approx 1.73)$

如图，某数学活动小组要测量建筑物 $\mathit{AB}$ 的高度，他们借助测角仪和皮尺进行了实地测量，测量结果如下表．

测量项目	测量数据
测角仪到地面的距离	$\mathit{CD}=1.6m$
点 $D$ 到建筑物的距离	$\mathit{BD}=4m$
从 $C$ 处观测建筑物顶部 $A$ 的仰角	$\angle \mathit{ACE}=67°$
从 $C$ 处观测建筑物底部 $B$ 的俯角	$\angle \mathit{BCE}=22°$

请根据需要，从上面表格中选择3个测量数据，并利用你选择的数据计算出建筑物 $\mathit{AB}$ 的高度．（结果精确到0.1米，参考数据： $\sin 67°\approx 0.92$ ， $\cos 67°\approx 0.39$ ， $\tan 67°\approx 2.36$ ． $\sin 22°\approx 0.37$ ， $\cos 22°\approx 0.93$ ， $\tan 22°\approx 0.40)$ （选择一种方法解答即可）

如图，某班数学小组测量塔的高度，在与塔底部 $B$ 相距 $35m$ 的 $C$ 处，用高 $1.5m$ 的测角仪 $\mathit{CD}$ 测得该塔顶端 $A$ 的仰角 $\angle \mathit{EDA}$ 为 $36°$ ．求塔 $\mathit{AB}$ 的高度（结果精确到 $1m)$ ．

（参考数据： $\sin 36°=0.59$ ， $\cos 36°=0.81$ ， $\tan 36°=0.73)$

我市在凤城河风景区举办了端午节赛龙舟活动，小亮在河畔的一幢楼上看到一艘龙舟迎面驶来，他在高出水面 $15m$ 的 $A$ 处测得在 $C$ 处的龙舟俯角为 $23°$ ；他登高 $6m$ 到正上方的 $B$ 处测得驶至 $D$ 处的龙舟俯角为 $50°$ ，问两次观测期间龙舟前进了多少？（结果精确到 $1m$ ，参考数据： $\tan 23°\approx 0.42$ ， $\tan 40°\approx 0.84$ ， $\tan 50°\approx 1.19$ ， $\tan 67°\approx 2.36)$

如图，某数学兴趣小组为测量一棵古树的高度，在距离古树 $A$ 点处测得古树顶端 $D$ 的仰角为 $30°$ ，然后向古树底端 $C$ 步行20米到达点 $B$ 处，测得古树顶端 $D$ 的仰角为 $45°$ ，且点 $A$ 、 $B$ 、 $C$ 在同一直线上，求古树 $\mathit{CD}$ 的高度．（已知： $\sqrt{2}\approx 1.414$ ， $\sqrt{3}\approx 1.732$ ，结果保留整数）

2020年5月5日，为我国载人空间站工程研制的长征五号运载火箭在海南文昌首飞成功．运载火箭从地面 $O$ 处发射，当火箭到达点 $A$ 时，地面 $D$ 处的雷达站测得 $\mathit{AD}=4000$ 米，仰角为 $30°$ ．3秒后，火箭直线上升到达点 $B$ 处，此时地面 $C$ 处的雷达站测得 $B$ 处的仰角为 $45°$ ．已知 $C$ ， $D$ 两处相距460米，求火箭从 $A$ 到 $B$ 处的平均速度（结果精确到1米 $/$ 秒，参考数据： $\sqrt{3}\approx 1.732$ ， $\sqrt{2}\approx 1.414)$ ．

如图，某楼房 $\mathit{AB}$ 顶部有一根天线 $\mathit{BE}$ ，为了测量天线的高度，在地面上取同一条直线上的三点 $C$ ， $D$ ， $A$ ，在点 $C$ 处测得天线顶端 $E$ 的仰角为 $60°$ ，从点 $C$ 走到点 $D$ ，测得 $\mathit{CD}=5$ 米，从点 $D$ 测得天线底端 $B$ 的仰角为 $45°$ ，已知 $A$ ， $B$ ， $E$ 在同一条垂直于地面的直线上， $\mathit{AB}=25$ 米．

（1）求 $A$ 与 $C$ 之间的距离；

（2）求天线 $\mathit{BE}$ 的高度．（参考数据： $\sqrt{3}\approx 1.73$ ，结果保留整数）

如图，是某小区的甲、乙两栋住宅楼，小丽站在甲栋楼房 $\mathit{AB}$ 的楼顶，测量对面的乙栋楼房 $\mathit{CD}$ 的高度．已知甲栋楼房 $\mathit{AB}$ 与乙栋楼房 $\mathit{CD}$ 的水平距离 $\mathit{AC}=18\sqrt{3}$ 米，小丽在甲栋楼房顶部 $B$ 点，测得乙栋楼房顶部 $D$ 点的仰角是 $30°$ ，底部 $C$ 点的俯角是 $45°$ ，求乙栋楼房 $\mathit{CD}$ 的高度（结果保留根号）．

鄂州市某校数学兴趣小组借助无人机测量一条河流的宽度．如图所示，一架水平飞行的无人机在处测得正前方河流的左岸处的俯角为，无人机沿水平线方向继续飞行50米至处，测得正前方河流右岸处的俯角为．线段的长为无人机距地面的铅直高度，点、、在同一条直线上．其中，米．

（1）求无人机的飞行高度；（结果保留根号）

（2）求河流的宽度．（结果精确到1米，参考数据：，