如图,小明利用学到的数学知识测量大桥主架在水面以上的高度 ,在观测点 处测得大桥主架顶端 的仰角为 ,测得大桥主架与水面交汇点 的俯角为 ,观测点与大桥主架的水平距离 为60米,且 垂直于桥面.(点 , , , 在同一平面内)
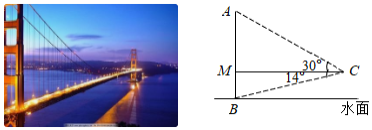
(1)求大桥主架在桥面以上的高度 ;(结果保留根号)
(2)求大桥主架在水面以上的高度 .(结果精确到1米)
(参考数据 , , ,
相关知识点
推荐套卷
如图,小明利用学到的数学知识测量大桥主架在水面以上的高度 ,在观测点 处测得大桥主架顶端 的仰角为 ,测得大桥主架与水面交汇点 的俯角为 ,观测点与大桥主架的水平距离 为60米,且 垂直于桥面.(点 , , , 在同一平面内)

(1)求大桥主架在桥面以上的高度 ;(结果保留根号)
(2)求大桥主架在水面以上的高度 .(结果精确到1米)
(参考数据 , , ,