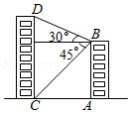
如图,是某小区的甲、乙两栋住宅楼,小丽站在甲栋楼房 的楼顶,测量对面的乙栋楼房 的高度.已知甲栋楼房 与乙栋楼房 的水平距离 米,小丽在甲栋楼房顶部 点,测得乙栋楼房顶部 点的仰角是 ,底部 点的俯角是 ,求乙栋楼房 的高度(结果保留根号).
相关知识点
推荐套卷
如图,是某小区的甲、乙两栋住宅楼,小丽站在甲栋楼房 的楼顶,测量对面的乙栋楼房 的高度.已知甲栋楼房 与乙栋楼房 的水平距离 米,小丽在甲栋楼房顶部 点,测得乙栋楼房顶部 点的仰角是 ,底部 点的俯角是 ,求乙栋楼房 的高度(结果保留根号).
