如果一条抛物线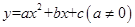 与
与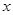 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.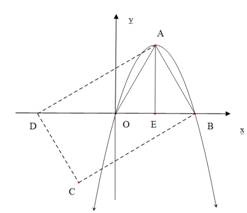
(1)“抛物线三角形”一定是 三角形;
(2)若抛物线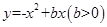 的“抛物线三角形”是等腰直角三角形,求
的“抛物线三角形”是等腰直角三角形,求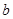 的值;
的值;
(3)如图,△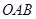 是抛物线
是抛物线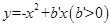 的“抛物线三角形”,是否存在以原点
的“抛物线三角形”,是否存在以原点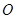 为对称中心的矩形
为对称中心的矩形 ?若存在,求出过
?若存在,求出过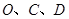 三点的抛物线的表达式;若不存在,说明理由.
三点的抛物线的表达式;若不存在,说明理由.
相关知识点
推荐套卷
如果一条抛物线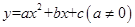 与
与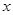 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(1)“抛物线三角形”一定是 三角形;
(2)若抛物线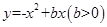 的“抛物线三角形”是等腰直角三角形,求
的“抛物线三角形”是等腰直角三角形,求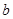 的值;
的值;
(3)如图,△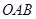 是抛物线
是抛物线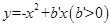 的“抛物线三角形”,是否存在以原点
的“抛物线三角形”,是否存在以原点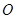 为对称中心的矩形
为对称中心的矩形 ?若存在,求出过
?若存在,求出过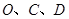 三点的抛物线的表达式;若不存在,说明理由.
三点的抛物线的表达式;若不存在,说明理由.