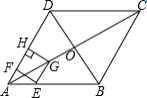
如图,在四边形 中,点 和点 是对角线 上的两点, , ,且 ,过点 作 交 的延长线于点 .
(1)求证:四边形 是平行四边形;
(2)若 , , ,则 的面积是 .

性质探究
如图①,在等腰三角形中,
,则底边
与腰
的长度之比为 .
理解运用
(1)若顶角为的等腰三角形的周长为
,则它的面积为 ;
(2)如图②,在四边形中,
.
①求证:;
②在边,
上分别取中点
,
,连接
.若
,
,直接写出线段
的长.
类比拓展
顶角为的等腰三角形的底边与一腰的长度之比为 (用含
的式子表示).

如图,在菱形中,对角线
与
相交于点
,
,
,点
从点
出发,沿
以每秒2个单位长度的速度向终点
运动,当点
不与点
重合时,过点
作
于点
,作
交
于点
,过点
作
交
(或
的延长线)于点
,得到矩形
,设点
运动的时间为
秒
(1)求线段的长(用含
的代数式表示);
(2)求点与点
重合时
的值;
(3)设矩形与菱形
重叠部分图形的面积与
平方单位,求
与
之间的函数关系式;
(4)矩形的对角线
与
相交于点
,当
时,
的值为 ;当
时,
的值为 .
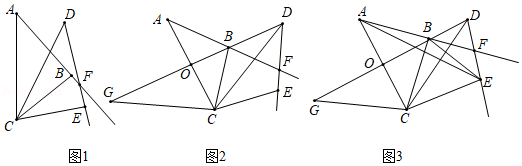
如图1, 绕点 顺时针旋转得 ,射线 交射线 于点 .
(1) 与 的关系是 ;
(2)如图2,当旋转角为 时,点 ,点 与线段 的中点 恰好在同一直线上,延长 至点 ,使 ,连接 .
① 与 的关系是 ,请说明理由;
②如图3,连接 , ,若 , ,求线段 的长度.
如图1和2,中,
,
,
.点
为
延长线上一点,过点
作
切
于点
,设
.
(1)如图1,为何值时,圆心
落在
上?若此时
交
于点
,直接指出
与
的位置关系;
(2)当时,如图2,
与
交于点
,求
的度数,并通过计算比较弦
与劣弧
长度的大小;
(3)当与线段
只有一个公共点时,直接写出
的取值范围.

如图,点在数轴上对应的数为26,以原点
为圆心,
为半径作优弧
,使点
在
右下方,且
,在优弧
上任取一点
,且能过
作直线
交数轴于点
,设
在数轴上对应的数为
,连接
.
(1)若优弧上一段
的长为
,求
的度数及
的值;
(2)求的最小值,并指出此时直线
与
所在圆的位置关系;
(3)若线段的长为12.5,直接写出这时
的值.

如图,点 是矩形 的边 延长线上一点,以 为直径的 交矩形对角
线 于点 ,在线段 上取一点 ,连接 ,使 .
(1)求证: 是 的切线;
(2)若 , , ,求 的长.

平面内,如图,在中,
,
,
,点
为
边上任意点,连接
,将
绕点
逆时针旋转
得到线段
.
(1)当时,求
的大小;
(2)当时,求点
与点
间的距离(结果保留根号);
(3)若点恰好落在
的边所在的直线上,直接写出
旋转到
所扫过的面积.(结果保留

在 中, , , 是 边上一点,且 , 是 的中点, 是 的中线.
(1)如图 ,连接 ,请直接写出 和 的数量关系: ;
(2)点 是射线 上的一个动点,将射线 绕点 逆时针旋转得射线 ,使 , 与射线 交于点 .
①如图 ,猜想并证明线段 和线段 之间的数量关系;
②若 , ,当 时,请直接写出线段 的长度(用含 的代数式表示).

如图,是
的直径,过
外一点
作
的两条切线
,
,切点分别为
,
,连接
,
.
(1)求证:;
(2)连接,
,若
,
,
,求
的长.

如图,已知 是 的直径, 是 所对的圆周角, .
(1)求 的度数;
(2)过点 作 ,垂足为 , 的延长线交 于点 .若 ,求 的长.

如图,AB为⊙O的弦,C为劣弧AB的中点.
(1)若⊙O的半径为5,AB=8,求tan∠BAC;
(2)若∠DAC=∠BAC,且点D在⊙O的外部,判断AD与⊙O的位置关系,并说明理由.
如图, 内接于 , 是 的直径,弦 与 交于点 ,连接 ,过点 作直线 ,使 .
(1)求证:直线 是 的切线.
(2)若 , , ,求 的长.

气象台发布的卫星云图显示,代号为W的台风在某海岛(设为点O)的南偏东450方向的B点生成,测得 。台风中心从点B以40km/h的速度向正北方向移动,经5h后到达海面上的点C处。因受气旋影响,台风中心从点C开始以30km/h的速度向北偏西600方向继续移动,以O为原点建立如图所示的直角坐标系。
。台风中心从点B以40km/h的速度向正北方向移动,经5h后到达海面上的点C处。因受气旋影响,台风中心从点C开始以30km/h的速度向北偏西600方向继续移动,以O为原点建立如图所示的直角坐标系。

(1)台风中心生成点B的坐标为( ),台风中心转折点C的坐标为( );(结果保留根号)
(2)已知距台风中心20km的范围内均会受到台风的侵袭.如果某城市(设为点A)位于点O的正北方向且处于台风中心的移动路线上,那么台风从生成到最初侵袭该城要经过多长时间?
如图,某大楼的顶部树有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度 ,AB=10米,AE=15米.
,AB=10米,AE=15米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据: )
)