性质探究
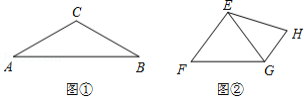
如图①,在等腰三角形中,,则底边与腰的长度之比为 .
理解运用
(1)若顶角为的等腰三角形的周长为,则它的面积为 ;
(2)如图②,在四边形中,.
①求证:;
②在边,上分别取中点,,连接.若,,直接写出线段的长.
类比拓展
顶角为的等腰三角形的底边与一腰的长度之比为 (用含的式子表示).
推荐套卷
性质探究
如图①,在等腰三角形中,,则底边与腰的长度之比为 .
理解运用
(1)若顶角为的等腰三角形的周长为,则它的面积为 ;
(2)如图②,在四边形中,.
①求证:;
②在边,上分别取中点,,连接.若,,直接写出线段的长.
类比拓展
顶角为的等腰三角形的底边与一腰的长度之比为 (用含的式子表示).
