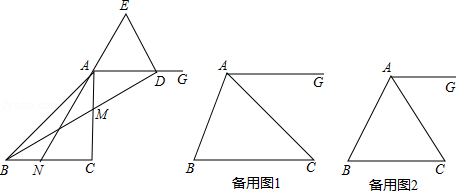
已知: 是等腰三角形, , .点 在边 上,点 在边 上(点 、点 不与所在线段端点重合), ,连接 , ,射线 ,延长 交射线 于点 ,点 在直线 上,且 .
(1)如图,当 时
①求证: ;
②求 的度数;
(2)当 ,其它条件不变时, 的度数是 ;(用含 的代数式表示)
(3)若 是等边三角形, ,点 是 边上的三等分点,直线 与直线 交于点 ,请直接写出线段 的长.
如图,某校数学兴趣小组的同学欲测量祁阳县文昌古塔BD的高度,他们先在A处测得古塔顶端点D的仰角为45°,再沿着BA的方向后退12米至C处,测得古塔顶端点D的仰角为30°.求该古塔BD的高度(结果保留根号).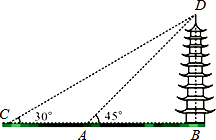
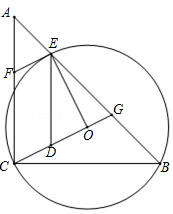
如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
(3)如果CD=15,BE=10,sinA= ,求⊙O的半径.
,求⊙O的半径.
如图,在 中, , , (圆心 在 内部)经过 、 两点,交 于点 ,过点 作 的切线交 于点 .延长 交 于点 ,作 交 于点
(1)求证:四边形 是平行四边形;
(2)若 , ,求 的值.
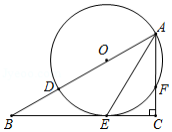
如图,在 中, ,点 在线段 上,以 为直径的 与 相交于点 ,与 相交于点 , .
(1)求证: 是 的切线;
(2)若 ,求 的半径 ;
(3)在(1)的条件下,判断以 、 、 、 为顶点的四边形为哪种特殊四边形,并说明理由.
某居民小区为缓解居民停车难问题为缓解“停车难”问题,拟造地下停车库,如图是地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5.根据规定,地下停车库破道口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.请根据以上数据,求出该地下停车库限高CE的长.(结果精确到0.1米)
(sin18°≈0.31,cos18°≈0.95,tan18°≈0.32) 
如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长(结果保留小数点后一位,参考数据: ≈1.41,
≈1.41, ≈1.73).
≈1.73).
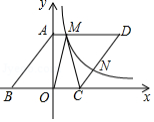
如图,菱形 的顶点 在 轴正半轴上,边 在 轴上,且 , ,反比例函数 的图象分别与 , 交于点 、点 ,点 的坐标是 ,连接 , .
(1)求反比例函数的解析式;
(2)求证: 是等腰三角形.
如图,在△ABC中,CD⊥AB,∠ACD=45°,∠DCB=60°,AC=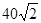 ,求AB.
,求AB.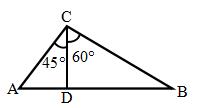
如图,抛物线 与 轴的负半轴交于点 ,与 轴交于点 ,连接 ,点 在抛物线上,直线 与 轴交于点 .
(1)求 的值及直线 的函数表达式;
(2)点 在 轴正半轴上,点 在 轴正半轴上,连接 与直线 交于点 ,连接 并延长交 于点 ,若 为 的中点.
①求证: ;
②设点 的横坐标为 ,求 的长(用含 的代数式表示).

在 中, ,点 是 的中点,点 是 上的一个动点(点 不与点 , , 重合).过点 ,点 作直线 的垂线,垂足分别为点 和点 ,连接 , .
(1)如图1,请直接写出线段 与 的数量关系;
(2)如图2,当 时,请判断线段 与 之间的数量关系和位置关系,并说明理由
(3)若 , ,当 为等腰三角形时,请直接写出线段 的长.

如图是一次“测量旗杆高度”的活动场景抽象出的平面几何图形.活动中测得的数据如下:
①小明的身高DC=1.5m
②小明的影长CE=1.7m
③小明的脚到旗杆底部的距离BC=9m
④旗杆的影长BF=7.6m
⑤从D点看A点的仰角为30°
你可以根据需要选出其中某几个数据,求出旗杆的高度.(计算结果保留到0.1,参考数据 ≈1.414,
≈1.414, ≈1.732)
≈1.732)
解:要想求旗杆的高度,你准备选择上面所给数据__________________(填序号);并写出求解过程.