湖南省永州市祁阳县九年级上学期期末教学质量检测数学试卷
已知∠A为锐角且tanA=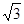 ,则∠A = ( )
,则∠A = ( )
| A.30° | B.45° | C.60° | D.不能确定 |
一元二次方程x2= -2x的根是( )
| A.x = 2 |
| B.x = -2 |
| C.x1 = 0,x2 = 2 |
| D.x1 = 0,x2 = -2 |
下列各点中,在函数 的图象上的点是( )
的图象上的点是( )
| A.(1,0.5) | B.(2,-1) |
| C.(-1,-2) | D.(-2,1) |
如图,△ABC内接于⊙O,CD是⊙O的直径,∠A =35°,则∠BCD的度数是( )
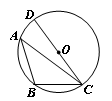
| A.55° | B.65° | C.70° | D.75° |
两个相似三角形的对应边分别是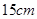 和
和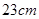 ,它们的周长相差
,它们的周长相差 ,则这两个三角形的周长分别是( )
,则这两个三角形的周长分别是( )
A. , , |
B.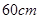 , ,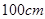 |
C.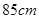 , ,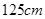 |
D.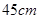 , ,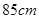 |
用配方法将二次函数y= x²-2x+1写成y=a(x-h)²+k的形式是( )
x²-2x+1写成y=a(x-h)²+k的形式是( )
A.y= (x-2)²-1 (x-2)²-1 |
B.y= (x-1)²-1 (x-1)²-1 |
C.y= (x-2)²-3 (x-2)²-3 |
D.y= (x-1)²-3 (x-1)²-3 |
根据下列表格的对应值:
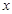 |
0.00 |
0.25 |
0.50 |
0.75 |
1.00 |
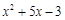 |
-3.00 |
-1.69 |
-0.25 |
1.31 |
3.00 |
可得方程x2+5x-3=0一个解x的范围是( )
A.0<x<0.25 B.0.25<x<0.50
C.0.50<x<0.75 D.0.75<x<1
某家用电器经过两次降价,每台零售价由1000元下降到810元.若两次降价的百分率相同,则这个百分率为 .
某水果店一次购进苹果200箱,已经卖出6箱,质量分别是(单位:kg)15.5,16,14.5,13.5,15,15.5.你估计该商店这次进货 kg.
在函数 (
(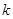 为常数)图象上有三个点(-2,y1),(-1,y2),(
为常数)图象上有三个点(-2,y1),(-1,y2),( ,y3),函数值y1,y2,y3的大小关系为 .(用“<”连接)
,y3),函数值y1,y2,y3的大小关系为 .(用“<”连接)
某校准备选出甲、乙两人中的一人参加县里的射击比赛,他们在相同条件下各射靶5次,成绩统计如下:
| 命中环数/环 |
7 |
8 |
9 |
10 |
| 甲命中的频数/次 |
1 |
1 |
0 |
3 |
| 乙命中的频数/次 |
0 |
1 |
3 |
1 |
(1)求甲、乙两人射击成绩的方差分别是多少?
(2)已知该校选手前三年都取得了县射击比赛的第一名,请问应选择谁去参加比赛?
已知:如图,在平面直角坐标系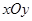 中,直线AB分别与
中,直线AB分别与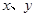 轴交于点B、A,与反比例函数的图象分别交于点C、D,
轴交于点B、A,与反比例函数的图象分别交于点C、D,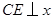 轴于点E,
轴于点E,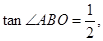
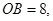
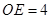 .求该反比例函数的解析式.
.求该反比例函数的解析式.
如图,某校数学兴趣小组的同学欲测量祁阳县文昌古塔BD的高度,他们先在A处测得古塔顶端点D的仰角为45°,再沿着BA的方向后退12米至C处,测得古塔顶端点D的仰角为30°.求该古塔BD的高度(结果保留根号).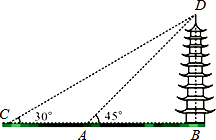
如图,已知AB为⊙O的直径,PA与⊙O相切于点A,线段OP与弦AC垂直并相交于点D,OP与⊙O相交于点E,连接BC.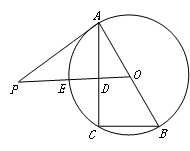
(1)求证:△PAD∽△ABC;
(2)若PA=10,AD=6,求AB的长.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.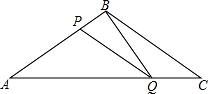
(1)当x为何值时,BP=CQ;
(2)以A、P、Q为顶点的三角形能否与以C、Q、B为顶点的三角形相似?若能,求出x的值;若不能,请说明理由.

 -4x+c与x轴只有一个交点,则c= .
-4x+c与x轴只有一个交点,则c= .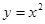 的图象向右平移1个单位,再向上平移2个单位后,所得图象的表达式是 .
的图象向右平移1个单位,再向上平移2个单位后,所得图象的表达式是 .
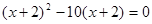
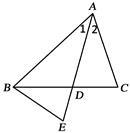
 的外接圆,
的外接圆, ,
, 为⊙O的直径,且
为⊙O的直径,且 ,连结
,连结 ,求BC的长.
,求BC的长.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号