在数学兴趣小组活动中,小亮进行数学探究活动. 是边长为2的等边三角形, 是 上一点,小亮以 为边向 的右侧作等边三角形 ,连接 .
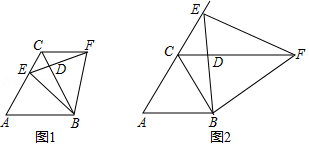
(1)如图1,当点 在线段 上时, 、 相交于点 ,小亮发现有两个三角形全等,请你找出来,并证明.
(2)当点 在线段 上运动时,点 也随着运动,若四边形 的面积为 ,求 的长.
(3)如图2,当点 在 的延长线上运动时, 、 相交于点 ,请你探求 的面积 与 的面积 之间的数量关系.并说明理由.
(4)如图2,当 的面积 时,求 的长.
如图,矩形 中,点 为对角线 所在直线上的一个动点,连接 ,过点 作 ,交直线 于点 ,过点 作 ,交直线 于点 ,交直线 于点 . , .
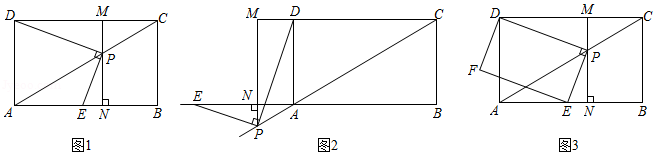
(1)如图1,①当点 在线段 上时, 和 的数量关系为: ;
② 的值是 ;
(2)如图2,当点 在 延长线上时,(1)中的结论②是否成立?若成立,请证明;若不成立,说明理由;
(3)如图3,以线段 , 为邻边作矩形 .设 的长为 ,矩形 的面积为 .请直接写出 与 之间的函数关系式及 的最小值.
如图1, 为 上一点,点 在直径 的延长线上,且 .
(1)判断直线 与 的位置关系,并说明理由;
(2)若 , ,求 的半径;
(3)如图2,在(2)的条件下, 的平分线 交 于点 ,交 于点 ,连结 .求 的值.

如图,矩形 中,点 为对角线 所在直线上的一个动点,连接 ,过点 作 ,交直线 于点 ,过点 作 ,交直线 于点 ,交直线 于点 . , .
(1)如图1,①当点 在线段 上时, 和 的数量关系为: ;
② 的值是 ;
(2)如图2,当点 在 延长线上时,(1)中的结论②是否成立?若成立,请证明;若不成立,说明理由;
(3)如图3,以线段 , 为邻边作矩形 .设 的长为 ,矩形 的面积为 .请直接写出 与 之间的函数关系式及 的最小值.

如图, 是 的内接三角形,点 在 上,点 在弦 上 不与 重合),且四边形 为菱形.
(1)求证: ;
(2)求证: ;
(3)已知 的半径为3.
①若 ,求 的长;
②当 为何值时, 的值最大?

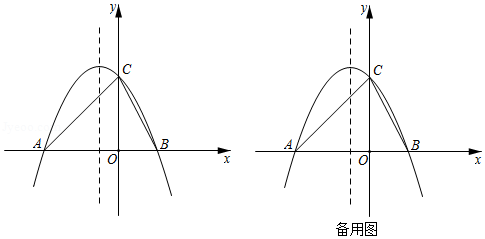
如图,抛物线 与 轴交于点 ,点 ,与 轴交于点 ,抛物线的对称轴为直线 ,点 坐标为 .
(1)求抛物线表达式;
(2)在抛物线上是否存在点 ,使 ,如果存在,求出点 坐标;如果不存在,请说明理由;
(3)在(2)的条件下,若点 在 轴上方,点 是直线 上方抛物线上的一个动点,求点 到直线 的最大距离;
(4)点 是线段 上的动点,点 是线段 上的动点,点 是线段 上的动点,三个动点都不与点 , , 重合,连接 , , ,得到 ,直接写出 周长的最小值.
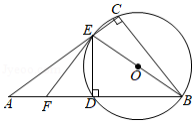
如图,在 中, , 的垂直平分线分别交 、 于点 、 , , 为 的外接圆,过点 作 的切线 交 于点 ,则下列结论正确的是 (写出所有正确结论的序号)
① ;
② ;
③若 ,则 的长为 ;
④ ;
⑤若 ,则 .
在 中, , .点 在直线 上,以 , 为边作矩形 ,直线 与直线 , 的交点分别为 , .
(1)如图,点 在线段 上,四边形 是正方形.
①若点 为 的中点,求 的长.
②若 ,求 的长.
(2)已知 ,是否存在点 ,使得 是等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.

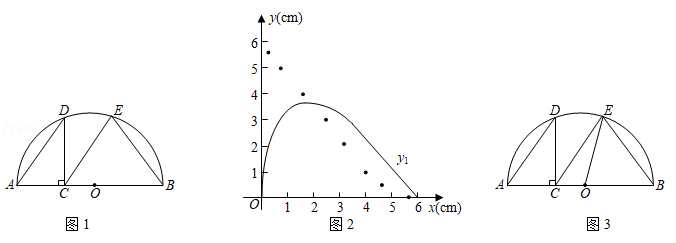
如图1,点 是半圆 的直径 上一动点(不包括端点), ,过点 作 交半圆于点 ,连结 ,过点 作 交半圆于点 ,连结 .牛牛想探究在点 运动过程中 与 的大小关系.他根据学习函数的经验,记 , , .请你一起参与探究函数 、 随自变量 变化的规律.
通过几何画板取点、画图、测量,得出如下几组对应值,并在图2中描出了以各对对应值为坐标的点,画出了不完整图象.
|
|
|
0.30 |
0.80 |
1.60 |
2.40 |
3.20 |
4.00 |
4.80 |
5.60 |
|
|
|
|
2.01 |
2.98 |
3.46 |
3.33 |
2.83 |
2.11 |
1.27 |
0.38 |
|
|
|
|
5.60 |
4.95 |
3.95 |
2.96 |
2.06 |
1.24 |
0.57 |
0.10 |
|
(1)当 时, .
(2)在图2中画出函数 的图象,并结合图象判断函数值 与 的大小关系.
(3)由(2)知" 取某值时,有 ".如图3,牛牛连结了 ,尝试通过计算 , 的长来验证这一结论,请你完成计算过程.
如图,在矩形 中,点 在边 上, 与 关于直线 对称,点 的对称点 在边 上, 为 中点,连结 分别与 , 交于 , 两点.若 , ,则 的长为 , 的值为 .

如图,点 在以 为直径的 上,过 作 的切线交 延长线于点 , 于点 ,交 于点 ,连接 , .
(1)求证: ;
(2)求证: ;
(3)若 , ,求 的长.

如图, 是 的内接三角形,过点 作 的切线交 的延长线于点 , 是 的直径,连接 .
(1)求证: ;
(2)若 , 于点 , , ,求 的值.

如图,在锐角三角形 中, 是 边上的高,以 为直径的 交 于点 ,交 于点 ,过点 作 ,垂足为 ,交 于点 ,交 于点 ,连接 , , .
(1)求证: ;
(2)若 , , ,求 的长.

如图, 是 的外接圆, 是 的直径, 于点 .
(1)求证: ;
(2)连接 并延长,交 于点 ,交 于点 ,连接 .若 的半径为5, ,求 和 的长.
