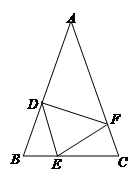
在数学兴趣小组活动中，小亮进行数学探究活动． 是边长为2的等边三角形， 是 上一点，小亮以 为边向 的右侧作等边三角形 ，连接 ．
（1）如图1，当点 在线段 上时， 、 相交于点 ，小亮发现有两个三角形全等，请你找出来，并证明．
（2）当点 在线段 上运动时，点 也随着运动，若四边形 的面积为 ，求 的长．
（3）如图2，当点 在 的延长线上运动时， 、 相交于点 ，请你探求 的面积 与 的面积 之间的数量关系．并说明理由．
（4）如图2，当 的面积 时，求 的长．
相关试题
如图，将长方形纸片ABCD沿着EF折叠，使得点C与点A重合．
（1）求证：AE=AF；
（2）若AB=3，BC=9，试求CF的长；
（3）在（2）的条件下，试求EF的长．
如图，在△ABC中，AB=AC，点D、E、F分别在AB、BC、AC边上，且BE=CF，BD=CE．
（1）求证：△DEF是等腰三角形；
（2）当∠A=40°时，求∠DEF的度数．
问题背景：在△ABC中，AB、BC、AC三边的长分别为
、
、
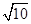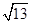，求这个三角形BC边上的高．辉辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处）．借用网格等知识就能计算出这个三角形BC边上的高．
（1）请在正方形网格中画出格点△ABC；
（2）求出这个三角形BC边上的高．
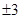，4x+2y+1的立方根是1，求4x-2y的平方根．相关知识点
推荐套卷
粤公网安备 44130202000953号