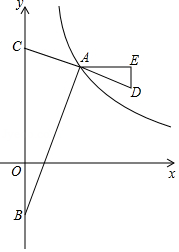
如图,在平面直角坐标系 中,点 是反比例函数 图象上一点,点 的横坐标为 ,点 是 轴负半轴上的一点,连接 , ,交 轴于点 ,延长 到点 ,使得 ,过点 作 平行于 轴,过点 作 轴平行线交 于点 .
(1)当 时,求点 的坐标;
(2) ,设点 的坐标为 ,求 关于 的函数关系式和自变量的取值范围;
(3)连接 ,过点 作 的平行线,与(2)中的函数图象交于点 ,当 为何值时,以 、 、 、 为顶点的四边形是平行四边形?
如图,锐角三角形 内接于 , 的平分线 交 于点 ,交 边于点 ,连接 .
(1)求证: .
(2)已知 , ,求线段 的长(用含 , 的代数式表示).
(3)已知点 在线段 上(不与点 ,点 重合),点 在线段 上(不与点 ,点 重合), ,求证: .

如图,直角 中, 为直角, , .点 , , 分别在 , , 边上同时开始作匀速运动,2秒后三个点同时停止运动,点 由点 出发以每秒3个单位的速度向点 运动,点 由点 出发以每秒5个单位的速度向点 运动,点 由点 出发以每秒4个单位的速度向点 运动,在运动过程中:
(1)求证: , , 的面积相等;
(2)求 面积的最小值;
(3)用 (秒 表示运动时间,是否存在 ,使 ?若存在,请直接写出 的值;若不存在,请说明理由.

如图,二次函数 的图象经过 , , 三点,以点 为位似中心,在 轴的右侧将 按相似比 放大,得到△ ,二次函数 的图象经过 , , 三点.
(1)画出△ ,试求二次函数 的表达式;
(2)点 在二次函数 的图象上, ,直线 与二次函数 的图象交于点 (异于点 .
①求点 的坐标(横、纵坐标均用含 的代数式表示)
②连接 ,若 ,求 的取值范围;
③当点 在第一象限内,过点 作 平行于 轴,与二次函数 的图象交于另一点 ,与二次函数 的图象交于点 , 在 的左侧),直线 与二次函数 的图象交于点 .△ △ ,则线段 的长度等于 .

已知,在 中, , , , 是 边上的一个动点,将 沿 所在直线折叠,使点 落在点 处.

(1)如图1,若点 是 中点,连接 .
①写出 , 的长;
②求证:四边形 是平行四边形.
(2)如图2,若 ,过点 作 交 的延长线于点 ,求 的长.
问题探究:
1.新知学习
若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”,其“面线”被该平面图形截得的线段叫做该平面图形的“面径”(例如圆的直径就是圆的“面径”).
2.解决问题

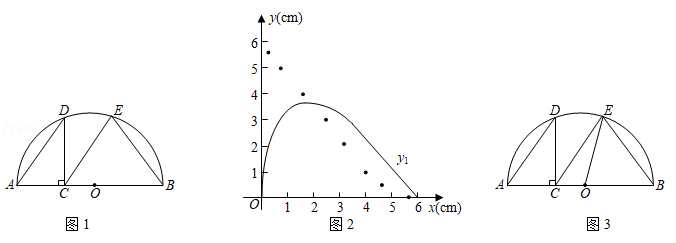
已知等边三角形ABC的边长为2.
(1)如图一,若 ,垂足为D,试说明AD是△ABC的一条面径,并求AD的长;
(2)如图二,若 ,且ME是△ABC的一条面径,求面径ME的长;
(3)如图三,已知D为BC的中点,连接AD,M为AB上的一点 ,E是DC上的一点,连接ME,ME与AD交于点O,且 .
①求证:ME是△ABC的面径;
②连接AE,求证: ;
(4)请你猜测等边三角形ABC的面径长l的取值范围(直接写出结果)
如图,将等腰直角三角形纸片 对折,折痕为 .展平后,再将点 折叠在边 上(不与 、 重合),折痕为 ,点 在 上的对应点为 ,设 与 交于点 ,连接 .已知 .
(1)若 为 的中点,求 的长;
(2)随着点 在边 上取不同的位置,
① 的形状是否发生变化?请说明理由;
②求 的周长的取值范围.

如图1,点 是半圆 的直径 上一动点(不包括端点), ,过点 作 交半圆于点 ,连结 ,过点 作 交半圆于点 ,连结 .牛牛想探究在点 运动过程中 与 的大小关系.他根据学习函数的经验,记 , , .请你一起参与探究函数 、 随自变量 变化的规律.
通过几何画板取点、画图、测量,得出如下几组对应值,并在图2中描出了以各对对应值为坐标的点,画出了不完整图象.
|
|
|
0.30 |
0.80 |
1.60 |
2.40 |
3.20 |
4.00 |
4.80 |
5.60 |
|
|
|
|
2.01 |
2.98 |
3.46 |
3.33 |
2.83 |
2.11 |
1.27 |
0.38 |
|
|
|
|
5.60 |
4.95 |
3.95 |
2.96 |
2.06 |
1.24 |
0.57 |
0.10 |
|
(1)当 时, .
(2)在图2中画出函数 的图象,并结合图象判断函数值 与 的大小关系.
(3)由(2)知" 取某值时,有 ".如图3,牛牛连结了 ,尝试通过计算 , 的长来验证这一结论,请你完成计算过程.
如图,在矩形 中,点 在边 上, 与 关于直线 对称,点 的对称点 在边 上, 为 中点,连结 分别与 , 交于 , 两点.若 , ,则 的长为 , 的值为 .

如图,点 在以 为直径的 上,过 作 的切线交 延长线于点 , 于点 ,交 于点 ,连接 , .
(1)求证: ;
(2)求证: ;
(3)若 , ,求 的长.

如图, 是 的内接三角形,过点 作 的切线交 的延长线于点 , 是 的直径,连接 .
(1)求证: ;
(2)若 , 于点 , , ,求 的值.

如图,在锐角三角形 中, 是 边上的高,以 为直径的 交 于点 ,交 于点 ,过点 作 ,垂足为 ,交 于点 ,交 于点 ,连接 , , .
(1)求证: ;
(2)若 , , ,求 的长.

如图, 是 的外接圆, 是 的直径, 于点 .
(1)求证: ;
(2)连接 并延长,交 于点 ,交 于点 ,连接 .若 的半径为5, ,求 和 的长.
