如图所示, 是 的直径,点 、 是 上不同的两点,直线 交线段 于点 、交过点 的直线 于点 ,若 ,且 .
(1)求证:直线 是 的切线;
(2)连接 、 、 、 ,若 .
①求证: ;
②过点 作 ,交线段 于点 ,点 为线段 的中点,若 ,求线段 的长度.

如图1, 是 的直径,点 是 上一动点,且不与 , 两点重合, 的平分线交 于点 ,过点 作 ,交 的延长线于点 .

(1)求证: 是 的切线;
(2)求证: ;
(3)如图2,原有条件不变,连接 , ,延长 至点 , 的平分线交 的延长线于点 , 的平分线交 的平分线于点 .求证:无论点 如何运动,总有 .
等面积法是一种常用的、重要的数学解题方法.它是利用“同一个图形的面积相等”、“分割图形后各部分的面积之和等于原图形的面积”、“同底等高或等底同高的两个三角形面积相等”等性质解决有关数学问题,在解题中,灵活运用等面积法解决相关问题,可以使解题思路清晰,解题过程简便快捷.
(1)在直角三角形中,两直角边长分别为3和4,则该直角三角形斜边上的高的长为 ,其内切圆的半径长为 ;
(2)①如图1, 是边长为 的正 内任意一点,点 为 的中心,设点 到 各边距离分别为 , , ,连接 , , ,由等面积法,易知 ,可得 ;(结果用含 的式子表示)

②如图2, 是边长为 的正五边形 内任意一点,设点 到五边形 各边距离分别为 , , , , ,参照①的探索过程,试用含 的式子表示 的值.(参考数据: ,
(3)①如图3,已知 的半径为2,点 为 外一点, , 切 于点 ,弦 ,连接 ,则图中阴影部分的面积为 ;(结果保留
②如图4,现有六边形花坛 ,由于修路等原因需将花坛进行改造,若要将花坛形状改造成五边形 ,其中点 在 的延长线上,且要保证改造前后花坛的面积不变,试确定点 的位置,并说明理由.

如图,在 中, ,点 在 边上,过 , , 三点的 交 边于另一点 ,且 是 的中点, 是 的一条直径,连接 并延长交 边于 点.
(1)求证:四边形 为平行四边形;
(2)当 时,求 的值.

如图, 、 是 的切线, 、 是切点, 是 的直径,连接 ,交 于点 ,交 于点 .
(1)求证: ;
(2)若 恰好是 的中点,且四边形 的面积是 ,求阴影部分的面积;
(3)若 ,且 ,求切线 的长.

如图,在 中, , 与 相交于点 ,与 相交于点 ,连接 ,已知 .
(1)求证: 为 的切线;
(2)若 , ,求 的长.

如图,在 中, ,以 为直径的 与 相交于点 , ,垂足为 .
(1)求证: 是 的切线;
(2)若弦 垂直于 ,垂足为 , , ,求 的半径;
(3)在(2)的条件下,当 时,求线段 的长.

如图,已知 是 的直径. 是 的弦,弦 垂直 于点 ,交 于点 .过点 作 的切线交 的延长线于点
(1)求证: ;
(2)判断 是否成立?若成立,请证明该结论;
(3)若 为 中点, , ,求 的长.
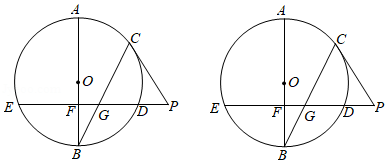
如图,一次函数 的图象与 轴的正半轴交于点 ,与反比例函数 的图象交于 , 两点.以 为边作正方形 ,点 落在 轴的负半轴上,已知 的面积与 的面积之比为 .
(1)求一次函数 的表达式;
(2)求点 的坐标及 外接圆半径的长.

如图, 的半径为6,将该圆周12等分后得到表盘模型,其中整钟点为 为 的整数),过点 作 的切线交 延长线于点 .
(1)通过计算比较直径和劣弧 长度哪个更长;
(2)连接 ,则 和 有什么特殊位置关系?请简要说明理由;
(3)求切线长 的值.

如图,已知 内接于 , 是 的直径, 的平分线交 于点 ,交 于点 ,连接 ,作 ,交 的延长线于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径和 的长.

如图,在 中, 为 的直径, 为 的弦,点 是 的中点,过点 作 的垂线,交 于点 ,交 于点 ,分别连接 , .
(1) 与 的数量关系是 ;
(2)求证: ;
(3)若 , ,求阴影部分图形的面积.

如图,四边形 中, , , , ,以 为圆心, 为半径作圆,延长 交 于点 ,延长 交 于点 ,连结 ,交 于点 .
(1)求证: 为 的切线;
(2)求 的值;
(3)求线段 的长.
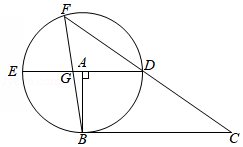
如图,在 中, , 是 上的一点,以 为直径的 与 相切于点 ,连接 , .
(1)求证: 平分 ;
(2)若 ,求 的值.
