如图,直线 经过 上的点 ,直线 与 交于点 和点 , 与 交于点 ,与 交于点 , , .
(1)求证: 是 的切线;
(2)若 , ,求图中阴影部分面积.

如图, 是 的直径, , 是 上两点, 是 的中点,过点 作 的垂线,垂足是 .连接 交 于点 .
(1)求证: 是 的切线;
(2)若 ,求 的值.

如图, 是以 为直径的 上一点,过点 的切线 交 的延长线于点 ,过点 作 交 的延长线于点 ,垂足为点 .
(1)求证: ;
(2)若 的直径 为9, .
①求线段 的长;
②求线段 的长.
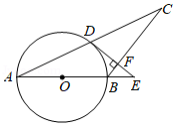
如图,已知 是 的直径, 为 上一点, 的角平分线交 于点 , 在直线 上,且 ,垂足为 ,连接 、 .
(1)求证: 是 的切线;
(2)若 , 的半径为3,求 的长.

如图,在 中, , 与 , 分别相切于点 , , 平分 ,连接 .
(1)求证: 是 的切线;
(2)若 , 的半径是1,求图中阴影部分的面积.

如图,在 中, , 为 边上一点,以 为圆心, 长为半径的 与 边相切于点 ,交 于点 .
(1)求证: ;
(2)连接 ,若 , ,求线段 的长.
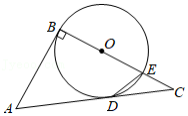
如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内, 的三个顶点坐标分别为 , , .
(1)画出 关于 轴对称的△ ,并写出点 的坐标;
(2)画出 绕点 顺时针旋转 后得到的△ ,并写出点 的坐标;
(3)在(2)的条件下,求点 旋转到点 所经过的路径长(结果保留 .
在古代,智慧的劳动人民已经会使用“石磨”,其原理为在磨盘的边缘连接一个固定长度的“连杆”,推动“连杆”带动磨盘转动,将粮食磨碎,物理学上称这种动力传输工具为“曲柄连杆机构”.
小明受此启发设计了一个“双连杆机构”,设计图如图1,两个固定长度的“连杆” , 的连接点 在 上,当点 在 上转动时,带动点 , 分别在射线 , 上滑动, .当 与 相切时,点 恰好落在 上,如图2.
请仅就图2的情形解答下列问题.
(1)求证: ;
(2)若 的半径为5, ,求 的长.

如图, 是以 为直径的 的切线,切点为 ,过点 作 ,交 于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.

如图, 与等边 的边 , 分别交于点 , , 是直径,过点 作 于点 .
(1)求证: 是 的切线;
(2)连接 ,当 是 的切线时,求 的半径 与等边 的边长 之间的数量关系.

如图, 是 的外接圆, 是 的直径, 是 延长线上一点,连接 , ,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.

(本题满分10分)
如图,点 在
在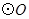 的直径
的直径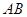 的延长线上,点
的延长线上,点 在
在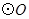 上,
上,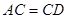 ,
,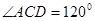 ,
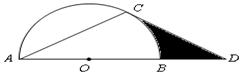
,
(1)求证:
 是
是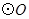 的切线;
的切线;(2)若
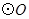 的半径为2,求图中阴影部分的面积.
的半径为2,求图中阴影部分的面积.
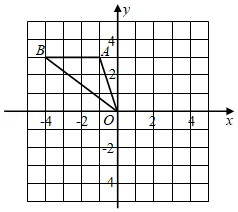
如图,在正方形网格图中建立直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1) 请在图中确定该圆弧所在圆心D点的位置,D点坐标为______;
(2) 连接AD、CD,求⊙D的半径及扇形ADC的圆心角度数;
(3) 若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径。