在四边形ABCD中,AD∥BC,且AD>BC,BC=6cm,P、Q分别从A、C
同时出发,P以1cm/s的速度由A向D运动,Q以2cm/s的速度由C出发向B运动,几
秒后四边形ABQP是平行四边形?
如图,在梯形ABCD中,AD∥BC,AB=AD+BC,E为CD的中点.
求证:AE⊥BE.
已知口ABCD中,M是边AB的中点,且BM=CM试说明四边形ABCD是矩形
已知正方形ABCD的边长是2,E是CD的中点,动点P从点A出发,沿A→B→C→E运动,到达E点即停止运动,若点P经过的路程为x,△APE的面积记为y,试求出y与x之间的函数解析式,并求出当y= 时,x的值.
时,x的值.
如图,D,E分别是△ABC的AB,AC边上的点,且DE∥BC,已知AD︰DB=1︰3, DE=2cm,求BC的长.
若△ADE的面积为1.5cm2,求梯形DBCE的面积.

已知如图,矩形OABC的长OA=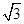 ,宽OC=1,
,宽OC=1,
将△AOC沿AC翻折得△APC.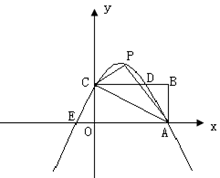
求∠PCB的度数
若P,A两点在抛物线y=-
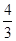 x2+bx+c上,求b,c的值,并 说明点C在此抛物线上;
x2+bx+c上,求b,c的值,并 说明点C在此抛物线上;(2)中的抛物线与矩形OABC边CB相交于点D,与x轴相交 于另外一点E,若点M是x轴上的点,N是y轴上的点,以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标.
如图1,在 中,
中,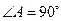 ,
,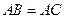 ,
,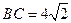 ,另有一等腰梯形
,另有一等腰梯形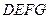 (
(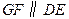 )的底边
)的底边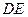 与
与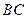 重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.
重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.
直接写出△AGF与△ABC的面积的比值;
操作:固定
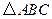 ,将等腰梯形
,将等腰梯形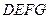 以每秒1个单位的速度沿
以每秒1个单位的速度沿 方向向右运动,直到点
方向向右运动,直到点 与点
与点 重合时停止.设运动时间为
重合时停止.设运动时间为 秒,运动后的等腰梯形为
秒,运动后的等腰梯形为 (如图2).
(如图2).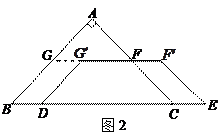
①探究1:在运动过程中,四边形 能否是菱形?若能,请求出此时
能否是菱形?若能,请求出此时 的值;若不能,请说明理由.
的值;若不能,请说明理由.
②探究2:设在运动过程中 与等腰梯形
与等腰梯形 重叠部分的面积为
重叠部分的面积为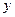 ,求
,求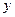 与
与 的函数关系式.
的函数关系式.
如图,在菱形ABCD中,AB=2cm,∠BAD=60°,E为CD边中点,点P从点A开始沿AC方向以每秒 cm的速度运动,同时,点Q从点D出发沿DB方向以每秒1cm的速度运动,当点P到达点C时,P,Q同时停止运动,设运动的时间为x秒.
cm的速度运动,同时,点Q从点D出发沿DB方向以每秒1cm的速度运动,当点P到达点C时,P,Q同时停止运动,设运动的时间为x秒.
当点P在线段AO上运动时.
①请用含x的代数式表示OP的长度;
②若记四边形PBEQ的面积为y,求y关于x的函数关系式(不要求写出自变量的取值范围)显然,当x=0时,四边形PBEQ即梯形ABED,请问,当P在线段AC的其他位置时,以P,B,E,Q为顶点的四边形能否成为梯形?若能,求出所有满足条件的x的值;若不能,请说明理由.
如图, 过
过 上到点
上到点 的距离为1,3,5,7,…的点作
的距离为1,3,5,7,…的点作 的垂线,分别与
的垂线,分别与 相交,得到图所示的阴影梯形,它们的面积依次记为
相交,得到图所示的阴影梯形,它们的面积依次记为 ….则
….则
 ;
;通过计算可得
 .
.
如图,在平面直角坐标系中有一矩形ABCO,B点的坐标为(12,6),点C、A在坐标轴上.⊙A、⊙P的半径均为1,点P从点C开始在线段CO上以1单位/秒的速度向左运动,运动到点O处停止.与此同时,⊙A的半径每秒钟增大2个单位,当点P停止运动时,⊙A的半径也停止变化.设点P运动的时间为t秒.在0<t<12时,设△OAP的面积为s,试求s与t的函数关系式.并求出当t为何值时,s为矩形ABCO面积的
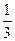 ;
;在点P的运动过程中,是否存在某一时刻,⊙A与⊙P相切,若存在求出点P的坐标,若不存在,说明理由.
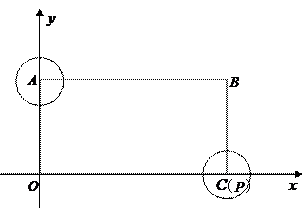
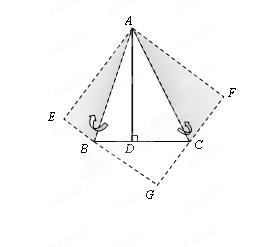
如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=4㎝,DC=6㎝,试求AD的长. 小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题。请按照小萍的思路,探究并解答下列问题:分别以AB、AC所在的直线为对称轴,画出△ABD、△ACD的轴对称图形,D点的对称点分别为点E、F,延长EB、FC相交于G点,试证明四边形AEGF是正方形;
设AD=x㎝,联系(1)的结论,试求出AD的长;
在直角梯形ABCD中,AB∥DC,AB⊥BC,∠A=60°,AB=2CD,E、F分别为AB、AD的中点,连结EF、EC、BF、CF.
判断四边形AECD的形状(不证明);
在不添加其它条件下,写出图中一对全等的三角形,用符号“≌”表示,并证明。
若CD=2,求梯形ABCD的面积。