2012届九年级第三次模拟考试数学卷
下列运算中,计算正确的是( )
| A.3x2+2x2="5x" 4 | B.(-x2)3=-x 6 | C.(2x2y)2=2x4y2 | D.(x+y2)2=x2+y4 |
一次数学测试后,随机抽取6名学生成绩如下:86,85,88,80,88,95,关于这组数据说法错误的是( )
| A.极差是15 | B.众数是88 | C.中位数是86 | D.平均数是87 |
2008年爆发的世界金融危机,是自上世纪三十年代以来世界最严重的一场金融危机。受金融危机的影响,某商品原价为200元,连续两次降价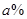 后售价为148元,下面所列方程正确的是( )
后售价为148元,下面所列方程正确的是( )
A.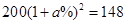 |
B.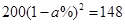 |
C.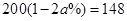 |
D.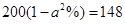 |
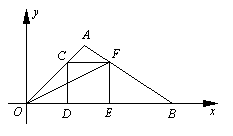
. 如图,已知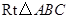 ,
,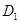 是斜边
是斜边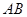 的中点,过
的中点,过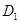 作
作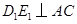 于
于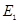 ,连结
,连结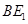 交
交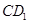 于
于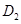 ;过
;过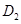 作
作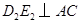 于
于 ,连结
,连结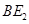 交
交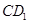 于
于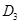 ;过
;过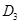 作
作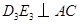 于
于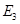 ,…,如此继续,可以依次得到点
,…,如此继续,可以依次得到点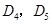 ,…,
,…,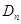 ,分别记
,分别记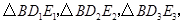 …,
…,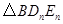 的面积为
的面积为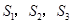 ,…
,…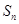 .则( )
.则( )
A.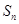 = =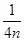 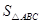 |
B.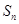 = =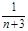 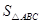 |
C.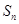 = =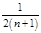 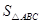 |
D.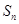 = =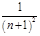 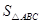 |
日本东部大地震造成日本国内经济损失约2350亿美元,其中2350亿保留两个有效数字用科学记数法表示为____________________.
下面图形:四边形、三角形、正方形、梯形、平行四边形、圆,从中任取一个图形既是轴 对称图形,又是中心对称图形的概率是 .
对称图形,又是中心对称图形的概率是 .
在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E, PF⊥AC于F,M为EF中点,则AM的最小值为 .
PF⊥AC于F,M为EF中点,则AM的最小值为 .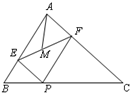
已知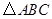 在平面直角坐标系中的位置如图所示.
在平面直角坐标系中的位置如图所示.
(1)分别写出图中点
 的坐标;
的坐标;(2)画出
 绕点
绕点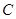 按顺时针方向旋转
按顺时针方向旋转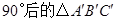 ;
;(3)求点
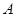 旋转到点
旋转到点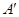 所经过的路线长(结果保留
所经过的路线长(结果保留 ).
).
为了进一步了解九年级500名学生的身体素质情况,体育老师对九年级(1)班50名学生进行一分钟跳绳次数测试,以测试数据为样本 ,绘制出部分频数分布表和部分频数分布直方图如下所示:
,绘制出部分频数分布表和部分频数分布直方图如下所示: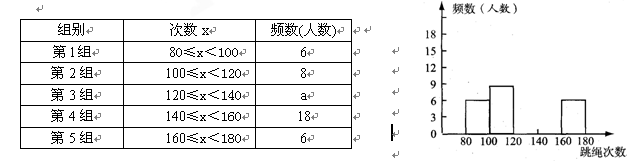
请结合图表完成下列问题: (1)表中的a=_
 _______,次数在140≤x<160 这组的频率为_________;
_______,次数在140≤x<160 这组的频率为_________; (2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第__________组;
(4)若九年级学生一分钟跳绳次数(x)达标要求是:x<120不合格;x≥120为合格,则这个年级合格的学生有_________人.
2011年4.18期间,扬州吸引了许多外地游客.小刚也随爸爸从上海来扬州游玩,由于仅有一天的时间,小刚不能游览所有风景区.于是爸爸让小刚上午从A.瘦西湖、B.茱萸湾风景区中任意选择一处游玩;下午从C.个园、D.何园、E.世界动物之窗中任意选一处 游玩.
游玩.⑴ 请用树状图或列表法说明小刚所有可能选择的方式(用字母表示);
⑵在⑴问的选择方式中,求小刚恰好选中A和E这两处的概率.
如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC,AF与CE的延长线相交于点F,连接BF.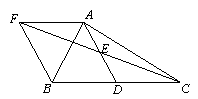
(1)求证:四边形AFBD是平行四边形;
(2)将下列命题填写完整,并使命题成立(图中不再添加其它的点和线):
① 当△ABC满足条件AB=AC时,四边形AFBD是 形;
② 当△ABC满足条件 时,四边形AFBD是正方形.
时,四边形AFBD是正方形.
如图,某广场一灯柱AB被一钢缆CD固定,CD与地面
成40°夹角,且CB =5米.
=5米.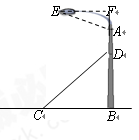
(1)求钢缆CD的长度;(精确到0.1米)
(2)若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米? (参考数据:tan400=0.84, sin400=0.64, cos400=
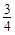 )
)
(本题满分10分)
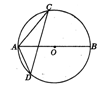
如图,点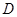 在
在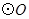 的直径
的直径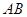 的延长线上,点
的延长线上,点 在
在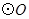 上,
上,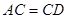 ,
,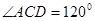 ,
,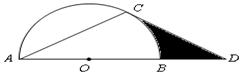
(1)求证:
 是
是 的切线;
的切线;(2)若
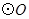 的半径为2,求图中阴影部分的面积.
的半径为2,求图中阴影部分的面积.
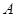 、
、 两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往
两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往 城,乙车驶往
城,乙车驶往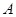 城,甲车在行驶过程中速度始终不变.甲车距
城,甲车在行驶过程中速度始终不变.甲车距 城高速公路入口处的距离
城高速公路入口处的距离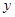 (千米)与行驶时间
(千米)与行驶时间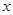 (时)之间的关系如图.
(时)之间的关系如图.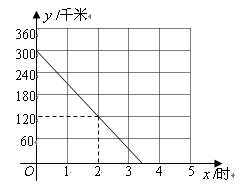
(1)求
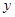 关于
关于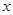 的表达式;
的表达式;(2)已知乙车以60千米/时的速度匀速行驶,设行驶过程中,相遇前两车相距的路程为
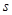 (千米).请直接写出
(千米).请直接写出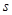 关于
关于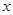 的表达式;
的表达式;(3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为
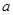 (千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度
(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度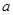 .在下图中画出乙车离开
.在下图中画出乙车离开 城高速公路入口处的距离
城高速公路入口处的距离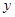 (千米)与行驶时间
(千米)与行驶时间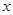 (时)之间的函数图象.
(时)之间的函数图象.
一家计算机专买店A型计算器每只进价12元,售价20元,多买优惠:凡是一次买10只以上的,每多买一只,所买的全部计算器每只就降低0.10元,例如,某人买20只计算器,于是每只降价0.10×(20-10)=1(元),因此,所买的全部20只计算器都按每只19元的价格购买.但是最低价为每只16元.(1)求一次至少买多少只,才能以最低价购买?
(2)写出专买店当一次销售x(x>10)只时,所获利润y元)与x(只)之间的函数关系式,并写出自变量x的取值范围;
(3)一天,甲买了46只,乙买了50只,店主却发现卖46只赚的钱反而比卖50只赚的钱多,你能用数学知识解释这一现象吗?为了不出现这种现象,在其他优惠条件不变的情况下,店家应把最低价每只16元至少提高到多少?
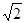 ,
,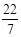 ,0.101001,
,0.101001,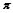 ,0,
,0,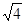 中,无理数的个数是( )
中,无理数的个数是( )
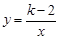 的图象位于第一、第三象
的图象位于第一、第三象 限,则k的取值范围是 ( )
限,则k的取值范围是 ( )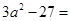 .
.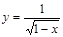 中自变量
中自变量 的取值范围是_______________.
的取值范围是_______________.
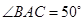 ,则
,则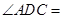 .
.
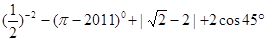
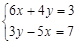
 值;
值; 粤公网安备 44130202000953号
粤公网安备 44130202000953号