初中数学圆解答题

如图，在梯形ABCD中，AB∥DC，DB平分∠ADC，过点A作AE∥BD，交CD的延长线于点E，且∠C＝2∠E．

（1）求证：梯形ABCD是等腰梯形．
（2）若∠BDC＝30°，AD＝5，求CD的长．

如图，已知BE⊥AD，CF⊥AD，且BE＝CF．
试判断AD是△ABC的中线还是角平分线？请证明你的结论．
连接BF、CE，若四边形BFCE是菱形，则△ABC中应添加的一个条件是          

如图，把一张矩形纸片ABCD沿对角线BD对折，使点C落在点E处，BE与AD交于点F.试判断重合部分图形的形状，并说明理由.

如图，四边形ABCD是菱形，DE⊥AB交BA的延长线于E，DF⊥BC，交BC的延长线于F．
求证：DE=DF

（本小题满分10分）已知：如图， ， 是□ABCD的对角线 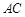上的两点， ，求证： ．

（本题7分）如图，E、F是平行四边形ABCD的对角线AC上的点，CE=AF，请你猜想：线段BE与线段DF有怎样的关系？并对你的猜想加以证明．

 

（本题5分）如图，在梯形ABCD中，AD∥BC，AB=DC=AD，AC=BC. 求∠B的度数．

 

如图，平行四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别为E、F．

写出图中每一对你认为全等的三角形
选择（1）中的任意一对进行证明

如图，在平行四边形ABCD中，E、F为对角线BD上的两点，且∠BAE=∠DCF．

试说明：AE∥CF
连接AF和CE，试说明四边形AFCE是平行四边形．

在我国古代数学著作《九章算术》中记载了一个有趣的问题，这个问题的意思是：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根新生的芦苇，它高出水面1尺，如图所示，如果把这根芦苇垂直拉向岸边，它的顶端恰好到达岸边的水面．那么水深多少？芦苇长为多少？

已知，如图，四边形ABCD中，∠ABC=∠ADC=90°，M、N分别是AC、BD的中点．
试证明：（1）MD=MB；
（2）MN⊥BD．

（本题5分）如图，在平行四边形ABCD中,对角线AC，BD相交于点O，且AE=CF，
则四边形DEBF是平行四边形吗?说明理由；

如图，BD是□ABCD的对角线，∠ABD的平分线BE交AD于点E，∠CDB的平分线DF交BC于点F．求证：四边形DEBF为平行四边形。

正方形ABCD与正方形CEFG的位置如图所示，点G在线段CD或CD的延长线上. 分别连接BD，BF，FD，得到△BFD.
（1）在图中，若正方形CEFG的边长分别为1，3，4，且正方形ABCD的边长均为3，请通过计算填写下表：

正方形CEFG的边长	1	3	4
△BFD的面积

（2）若正方形CEFG的边长为a，正方形ABCD的边长为b，猜想S_△BFD的大小，并结合图3证明你的猜想.

如图11-①，为的直径，与相切于点与相切于点，点为延长线上一点，且

（1）求证：为的切线；
（2）连接，的延长线与的延长线交于点（如图11-②所示）.若，求线段和的长.