实验探究:
(1)如图1,对折矩形纸片 ,使 与 重合,得到折痕 ,把纸片展开;再一次折叠纸片,使点 落在 上,并使折痕经过点 ,得到折痕 ,同时得到线段 , .请你观察图1,猜想 的度数是多少,并证明你的结论.
(2)将图1中的三角形纸片 剪下,如图2.折叠该纸片,探究 与 的数量关系.写出折叠方案,并结合方案证明你的结论.
如图,在 中, 为直径,点 为圆上一点,延长 到点 ,使 ,且 .
(1)求证: 是 的切线.
(2)分别过 、 两点作直线 的垂线,垂足分别为 、 两点,过 点作 的垂线,垂足为点 .求证: .

如图,矩形 中, 是 的中点,延长 , 交于点 ,连接 , .
(1)求证:四边形 是平行四边形;
(2)当 平分 时,写出 与 的数量关系,并说明理由.

如图1,在等腰直角三角形 中, , .点 是 的中点,以 为边作正方形 ,连接 , .将正方形 绕点 顺时针旋转,旋转角为 .
(1)如图2,在旋转过程中,
①判断 与 是否全等,并说明理由;
②当 时, 与 交于点 ,求 的长.
(2)如图3,延长 交直线 于点 .
①求证: ;
②在旋转过程中,线段 的长度是否存在最大值?若存在,求出最大值;若不存在,请说明理由.

如图1, 的边 在 轴的正半轴上, , ,反比例函数 的图象经过的 .

(1)求点 的坐标和反比例函数的关系式;
(2)如图2,直线 分别与 轴、 轴的正半轴交于 , 两点,若点 和点 关于直线 成轴对称,求线段 的长;
(3)如图3,将线段 延长交 的图象于点 ,过 , 的直线分别交 轴、 轴于 , 两点,请探究线段 与 的数量关系,并说明理由.
已知:点P是平行四边形ABCD对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BD作垂线,垂足分别为点E、F,点O为AC的中点.
(1)当点P与点O重合时如图1,易证 (不需证明)
(2)直线BP绕点B逆时针方向旋转,当 时,如图2、图3的位置,猜想线段CF、AE、OE之间有怎样的数量关系?请写出你对图2、图3的猜想,并选择一种情况给予证明.

如图,在 中,弦 与直径 垂直,垂足为 , 的延长线上有
一点 ,满足 .过点 作 ,交 的延长线于点 ,连接 交 于点 .
(1)求证: 是 的切线;
(2)如果 , ,求 的值;
(3)如果 ,求证: .

已知:点P是平行四边形ABCD对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BD作垂线,垂足分别为点E、F,点O为AC的中点.
(1)当点P与点O重合时如图1,易证 (不需证明)
(2)直线BP绕点B逆时针方向旋转,当 时,如图2、图3的位置,猜想线段CF、AE、OE之间有怎样的数量关系?请写出你对图2、图3的猜想,并选择一种情况给予证明.

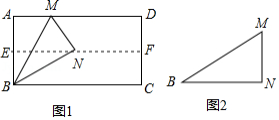
在▱ABCD中,点P和点Q是直线BD上不重合的两个动点, ,AD=BD.
(1)如图①,求证: ;
(2)请直接写出图②,图③中BP、BQ、BC三者之间的数量关系,不需要证明;
(3)在(1)和(2)的条件下,若 , ,则BC= .
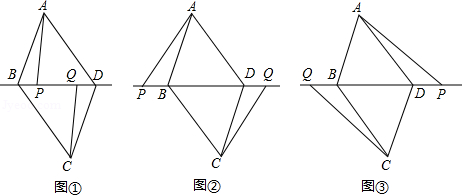
如图,在 的边 上取一点 ,以 为圆心, 为半径画 , 与边 相切于点 , ,连接 交 于点 ,连接 ,并延长交线段 于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径;
(3)若 是 的中点,试探究 与 的数量关系并说明理由.
在Rt△ABC中, ,点D为斜边AB的中点, , ,过点A作 且 ,过点E作EF垂直于AC边所在的直线,垂足为点F,连接DF,请你画出图形,并直接写出线段DF的长.
已知:如图,在正方形 ABCD中,点 E在边 CD上, 于点 Q, 于点 P.
(1)求证: ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于 PQ的长.

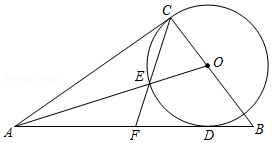
如图,在Rt△ ABC中,∠ C=90°,以 BC为直径的⊙ O交斜边 AB于点 M,若 H是 AC的中点,连接 MH.
(1)求证: MH为⊙ O的切线.
(2)若 ,求⊙ O的半径.
(3)在(2)的条件下分别过点 A、 B作⊙ O的切线,两切线交于点 D, AD与⊙ O相切于 N点,过 N点作 NQ⊥ BC,垂足为 E,且交⊙ O于 Q点,求线段 NQ的长度.
