如图1, 的边 在 轴的正半轴上, , ,反比例函数 的图象经过的 .
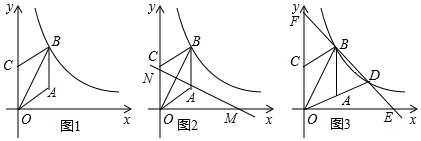
(1)求点 的坐标和反比例函数的关系式;
(2)如图2,直线 分别与 轴、 轴的正半轴交于 , 两点,若点 和点 关于直线 成轴对称,求线段 的长;
(3)如图3,将线段 延长交 的图象于点 ,过 , 的直线分别交 轴、 轴于 , 两点,请探究线段 与 的数量关系,并说明理由.
推荐套卷
如图1, 的边 在 轴的正半轴上, , ,反比例函数 的图象经过的 .

(1)求点 的坐标和反比例函数的关系式;
(2)如图2,直线 分别与 轴、 轴的正半轴交于 , 两点,若点 和点 关于直线 成轴对称,求线段 的长;
(3)如图3,将线段 延长交 的图象于点 ,过 , 的直线分别交 轴、 轴于 , 两点,请探究线段 与 的数量关系,并说明理由.