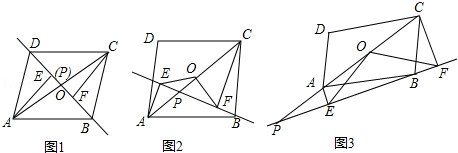
已知：点P是平行四边形ABCD对角线AC所在直线上的一个动点

首页 / 初中数学 / 试题详细

已知：点P是平行四边形ABCD对角线AC所在直线上的一个动点（点P不与点A、C重合），分别过点A、C向直线BD作垂线，垂足分别为点E、F，点O为AC的中点．

（1）当点P与点O重合时如图1，易证 $OE ＝ OF$ （不需证明）

（2）直线BP绕点B逆时针方向旋转，当 $∠ OFE ＝ 30 °$ 时，如图2、图3的位置，猜想线段CF、AE、OE之间有怎样的数量关系？请写出你对图2、图3的猜想，并选择一种情况给予证明．

相关试题

如图所示， $△ A_{1} B_{1} C_{1}$ 是由 $△ ABC$ 平移后得到的，已知 $△ ABC$ 中任意一点 $P (x_{0} ， y_{0})$ 经平移后对应点为 $P_{1} (x_{0} - 6 ， y_{0} - 2)$ .

（1）已知 $A (2 ， 6) ， B (1 ， 3) ， C (5 ， 3) ， Q (3 ， 5)$ ，请写出 $A_{1} ， B_{1} ， C_{1} ， Q_{1}$ 的坐标

（2）试说明 $△ A_{1} B_{1} C_{1}$ 是如何由 $△ ABC$ 得到的?

（3）连接 $A_{1} A ， C_{1} C$ ，求出五边形 $A_{1} B_{1} C_{1} CA$ 的面积.

收藏答案/解析

已知 $\sqrt{a^{2} + 2005}$ 是整数，求所有满足条件的正整数 $a$ 的和.

收藏答案/解析

已知 $a ， b ， c$ 为正整数，且 $\frac{\sqrt{3} a + b}{\sqrt{3} b + c}$ 为有理数，证明： $\frac{a^{2} + b^{2} + c^{2}}{a + b + c}$ 为整数.

收藏答案/解析

若有理数 $x ， y ， z$ 满足 $\sqrt{x} + \sqrt{y - 1} + \sqrt{z - 2} = \frac{1}{2} (x + y + z)$ ，试确定 ${(x - y z)}^{3}$ 的值.

收藏答案/解析

若 $m$ 满足关系式 $\sqrt{3 x + 5 y - 2 - m} + \sqrt{2 x + 3 y - m} = \sqrt{x + y - 1} \cdot \sqrt{1 - x - y}$ ，求 $m$ 的值.

收藏答案/解析

相关知识点

平行四边形的性质几何变换综合题全等三角形的判定与性质四边形综合题

推荐套卷

热门套卷

粤ICP备20024846号

声明：本网站部分内容由互联网用户自发贡献自行上传，本网站不拥有所有权，也不承担相关法律责任。
如果您发现有涉嫌版权的内容，欢迎发送邮件至：service@youtike.com 或联系QQ：267757 进行举报，一经查实，本站将立刻删除涉嫌侵权内容。