如图, 中, 为钝角, ,点 是边 延长线上一点,以点 为顶点, 为边,在射线 下方作 .
(1)在射线 上取点 ,连接 交线段 于点 .
①如图1,若 ,请直接写出线段 与 的数量关系和位置关系;
②如图2,若 ,判断线段 与 的数量关系和位置关系,并说明理由;
(2)如图3,反向延长射线 ,交射线 于点 ,将 沿 方向平移,使顶点 落在点 处,记平移后的 为 ,将 绕点 顺时针旋转角 , 交线段 于点 , 交射线 于点 ,请直接写出线段 , 与 之间的数量关系.

在中,
,
,
是
上一点,连接
.
(1)如图1,若,
是
延长线上一点,
与
垂直,求证:
.
(2)过点作
,
为垂足,连接
并延长交
于点
.
①如图2,若,求证:
.
②如图3,若是
的中点,直接写出
的值.(用含
的式子表示)

已知:如图,在正方形 ABCD中,点 E在边 CD上, 于点 Q, 于点 P.
(1)求证: ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于 PQ的长.

已知在 中, , , , 分别为 , 边上的点(不包括端点),且 ,连接 ,过点 作 ,垂足为点 ,延长 交 于点 .
(1)如图1,过点 作 于点 ,连接 .
①求证:四边形 是平行四边形;
②若 ,求证: ;
(2)如图2,若 ,求 的值.

如图,在Rt△ ABC中,∠ C=90°,以 BC为直径的⊙ O交斜边 AB于点 M,若 H是 AC的中点,连接 MH.
(1)求证: MH为⊙ O的切线.
(2)若 ,求⊙ O的半径.
(3)在(2)的条件下分别过点 A、 B作⊙ O的切线,两切线交于点 D, AD与⊙ O相切于 N点,过 N点作 NQ⊥ BC,垂足为 E,且交⊙ O于 Q点,求线段 NQ的长度.

如图,在菱形 ABCD中, G是 BD上一点,连接 CG并延长交 BA的延长线于点 F,交 AD于点 E.
(1)求证: AG= CG.
(2)求证: AG 2= GE• GF.
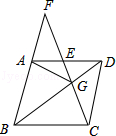
如图,在平行四边形 中,对角线 , 相交于点 ,分别过点 , 作 , ,垂足分别为 , . 平分 .
(1)若 ,求 的度数;
(2)求证: .

杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:

如图, ,相邻两平行线间的距离相等,AC,BD相交于O, .垂足为D,已知 米,请根据上述信息求标语CD的长度.
如图, 和 是有公共顶点的等腰直角三角形, ,点 为射线 , 的交点.
(1)求证: ;
(2)若 , ,把 绕点 旋转,当 时,求 的长;
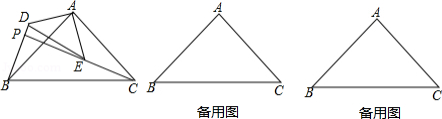
如图,在△ABC中,AD平分∠BAC,且 , 于点E, 于点F.
(1)求证: ;
(2)若 , ,求AC的长.
