初中数学三角形解答题

如图，点 $M$， $N$分别在正三角形 $\mathit{ABC}$的 $\mathit{BC}$， $\mathit{CA}$边上，且 $\mathit{BM}=\mathit{CN}$， $\mathit{AM}$， $\mathit{BN}$交于点 $Q$．求证： $\angle \mathit{BQM}=60°$．

如图，四边形 $\mathit{ABCD}$是菱形， $\mathit{CE}\perp \mathit{AB}$交 $\mathit{AB}$的延长线于点 $E$， $\mathit{CF}\perp \mathit{AD}$交 $\mathit{AD}$的延长线于点 $F$，求证： $\mathit{DF}=\mathit{BE}$．

如图，点 $D$是等边三角形 $\mathit{ABC}$外接圆上一点． $M$是 $\mathit{BD}$上一点，且满足 $\mathit{DM}=\mathit{DC}$，点 $E$是 $\mathit{AC}$与 $\mathit{BD}$的交点．

（1）求证： $\mathit{CM}//\mathit{AD}$；

（2）如果 $\mathit{AD}=1$， $\mathit{CM}=2$．求线段 $\mathit{BD}$的长及 $\mathit{\Delta BCE}$的面积．

如图，在四边形 $\mathit{ABCF}$中， $\angle \mathit{ACB}=90°$，点 $E$是 $\mathit{AB}$边的中点，点 $F$恰是点 $E$关于 $\mathit{AC}$所在直线的对称点．

（1）证明：四边形 $\mathit{CFAE}$为菱形；

（2）连接 $\mathit{EF}$交 $\mathit{AC}$于点 $O$，若 $\mathit{BC}=10$，求线段 $\mathit{OF}$的长．

$\mathit{\Delta ABC}$中， $\angle \mathit{BAC}=90°$， $\mathit{AB}=\mathit{AC}$，点 $D$为直线 $\mathit{BC}$上一动点（点 $D$不与 $B$， $C$重合），以 $\mathit{AD}$为边在 $\mathit{AD}$右侧作正方形 $\mathit{ADEF}$，连接 $\mathit{CF}$．

（1）观察猜想

如图1，当点 $D$在线段 $\mathit{BC}$上时，

① $\mathit{BC}$与 $\mathit{CF}$的位置关系为：　　．

② $\mathit{BC}$， $\mathit{CD}$， $\mathit{CF}$之间的数量关系为：　　；（将结论直接写在横线上）

（2）数学思考

如图2，当点 $D$在线段 $\mathit{CB}$的延长线上时，结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．

（3）拓展延伸

如图3，当点 $D$在线段 $\mathit{BC}$的延长线上时，延长 $\mathit{BA}$交 $\mathit{CF}$于点 $G$，连接 $\mathit{GE}$．若已知 $\mathit{AB}=2\sqrt{2}$， $\mathit{CD}=\frac{1}{4}\mathit{BC}$，请求出 $\mathit{GE}$的长．

如图①， $\mathit{\Delta ABC}$中， $\angle \mathit{ABC}=45°$， $\mathit{AH}\perp \mathit{BC}$于点 $H$，点 $D$在 $\mathit{AH}$上，且 $\mathit{DH}=\mathit{CH}$，连接 $\mathit{BD}$．

（1）求证： $\mathit{BD}=\mathit{AC}$；

（2）将 $\mathit{\Delta BHD}$绕点 $H$旋转，得到 $\mathit{\Delta EHF}$（点 $B$， $D$分别与点 $E$， $F$对应），连接 $\mathit{AE}$．

①如图②，当点 $F$落在 $\mathit{AC}$上时， $(F$不与 $C$重合），若 $\mathit{BC}=4$， $\tan C=3$，求 $\mathit{AE}$的长；

②如图③，当 $\mathit{\Delta EHF}$是由 $\mathit{\Delta BHD}$绕点 $H$逆时针旋转 $30°$得到时，设射线 $\mathit{CF}$与 $\mathit{AE}$相交于点 $G$，连接 $\mathit{GH}$，试探究线段 $\mathit{GH}$与 $\mathit{EF}$之间满足的等量关系，并说明理由．

如图，方格中，每个小正方形的边长都是单位1， $\mathit{\Delta ABC}$在平面直角坐标系中的位置如图．

（1）画出将 $\mathit{\Delta ABC}$向右平移2个单位得到△ $A_1{B}_1{C}_1$；

（2）画出将 $\mathit{\Delta ABC}$绕点 $O$顺时针方向旋转 $90°$得到的△ $A_2{B}_2{C}_2$；

（3）求△ $A_1{B}_1{C}_1$与△ $A_2{B}_2{C}_2$重合部分的面积．

已知：如图，四边形 $\mathit{ABCD}$是平行四边形，延长 $\mathit{BA}$至点 $E$，使 $\mathit{AE}+\mathit{CD}=\mathit{AD}$．连接 $\mathit{CE}$，求证： $\mathit{CE}$平分 $\angle \mathit{BCD}$．

如图①， $\mathit{AD}$为等腰直角 $\mathit{\Delta ABC}$的高，点 $A$和点 $C$分别在正方形 $\mathit{DEFG}$的边 $\mathit{DG}$和 $\mathit{DE}$上，连接 $\mathit{BG}$， $\mathit{AE}$．

（1）求证： $\mathit{BG}=\mathit{AE}$；

（2）将正方形 $\mathit{DEFG}$绕点 $D$旋转，当线段 $\mathit{EG}$经过点 $A$时，（如图②所示）

①求证： $\mathit{BG}\perp \mathit{GE}$；

②设 $\mathit{DG}$与 $\mathit{AB}$交于点 $M$，若 $\mathit{AG}:\mathit{AE}=3:4$，求 $\frac{\mathit{GM}}{\mathit{MD}}$的值．

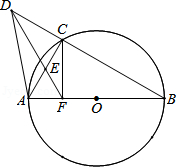
已知AB是半径为1的圆O直径，C是圆上一点，D是BC延长线上一点，过点D的直线交AC于E点，且△AEF为等边三角形

（1）求证：△DFB是等腰三角形；

（2）若 $\mathit{DA}＝\sqrt{7}\mathit{AF}$，求证： $\mathit{CF}\perp \mathit{AB}$．

已知正方形ABCD中， $\mathit{BC}＝3$，点E、F分别是CB、CD延长线上的点，DF＝BE，连接AE、AF，过点A作 $\mathit{AH}\perp \mathit{ED}$于H点．

（1）求证： $△\mathit{ADF}≌△\mathit{ABE}$；

（2）若 $\mathit{BE}＝1$，求 $\mathit{tan}\angle \mathit{AED}$的值．

已知：如图，在四边形ABCD中， $\mathit{AB}\parallel \mathit{CD}$，E是BC的中点，直线AE交DC的延长线于点F．试判断四边形ABFC的形状，并证明你的结论．

已知：如图，在矩形ABCD中，点E在边AB上，点F在边BC上，且 $\mathit{BE}＝\mathit{CF}$， $\mathit{EF}\perp \mathit{DF}$，求证： $\mathit{BF}＝\mathit{CD}$．

问题探究：

1．新知学习

若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”，其“面线”被该平面图形截得的线段叫做该平面图形的“面径”（例如圆的直径就是圆的“面径”）．

2．解决问题

已知等边三角形ABC的边长为2．

（1）如图一，若 $\mathit{AD}\perp \mathit{BC}$，垂足为D，试说明AD是△ABC的一条面径，并求AD的长；

（2）如图二，若 $\mathit{ME}\parallel \mathit{BC}$，且ME是△ABC的一条面径，求面径ME的长；

（3）如图三，已知D为BC的中点，连接AD，M为AB上的一点 $（0＜\mathit{AM}＜1）$，E是DC上的一点，连接ME，ME与AD交于点O，且 $S_{△\mathit{MOA}}＝S_{△\mathit{DOE}}$．

①求证：ME是△ABC的面径；

②连接AE，求证： $\mathit{MD}\parallel \mathit{AE}$；

（4）请你猜测等边三角形ABC的面径长l的取值范围（直接写出结果）

如图，△ABC是⊙O的内接三角形，AB为直径，过点B的切线与AC的延长线交于点D，E是BD中点，连接CE．

（1）求证：CE是⊙O的切线；

（2）若AC＝4，BC＝2，求BD和CE的长．