初中数学三角形解答题

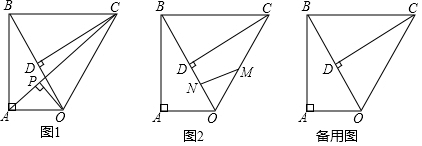
如图，在Rt△ ABC中，∠ C＝90°，以 BC为直径的⊙ O交斜边 AB于点 M，若 H是 AC的中点，连接 MH．

（1）求证： MH为⊙ O的切线．

（2）若 $\mathit{MH}=\frac{3}{2},$ $\tan \angle \mathit{ABC}=\frac{3}{4}$ ，求⊙ O的半径．

（3）在（2）的条件下分别过点 A、 B作⊙ O的切线，两切线交于点 D， AD与⊙ O相切于 N点，过 N点作 NQ⊥ BC，垂足为 E，且交⊙ O于 Q点，求线段 NQ的长度．

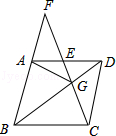
如图，在菱形 ABCD中， G是 BD上一点，连接 CG并延长交 BA的延长线于点 F，交 AD于点 E．

（1）求证： AG＝ CG．

（2）求证： AG ²＝ GE• GF．

杨阳同学沿一段笔直的人行道行走，在由A步行到达B处的过程中，通过隔离带的空隙O，刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语，其具体信息汇集如下：

如图， $\mathit{AB}\parallel \mathit{OH}\parallel \mathit{CD}$，相邻两平行线间的距离相等，AC，BD相交于O， $\mathit{OD}\perp \mathit{CD}$．垂足为D，已知 $\mathit{AB}＝20$米，请根据上述信息求标语CD的长度．

如图，在Rt△ABC中， $\angle \mathit{ACB}＝90°$．

（1）请用直尺和圆规按下列步骤作图，保留作图痕迹：

①作∠ACB的平分线，交斜边AB于点D；

②过点D作AC的垂线，垂足为点E．

（2）在（1）作出的图形中，若 $\mathit{CB}＝4$， $\mathit{CA}＝6$，则DE＝　　．

如图， $\mathit{BD}\perp \mathit{AC}$于点D， $\mathit{CE}\perp \mathit{AB}$于点E， $\mathit{AD}＝\mathit{AE}$．求证： $\mathit{BE}＝\mathit{CD}$．

如图，在△ABC中，AD平分∠BAC，且 $\mathit{BD}＝\mathit{CD}$， $\mathit{DE}\perp \mathit{AB}$于点E， $\mathit{DF}\perp \mathit{AC}$于点F．

（1）求证： $\mathit{AB}＝\mathit{AC}$；

（2）若 $\mathit{AD}=2\sqrt{3}$， $\angle \mathit{DAC}＝30°$，求AC的长．

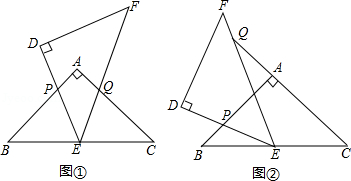
△ABC和△DEF是两个全等的等腰直角三角形， $\angle \mathit{BAC}＝\angle \mathit{EDF}＝90°$，△DEF的顶点E与△ABC的斜边BC的中点重合，将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．

（1）如图①，当点Q在线段AC上，且 $\mathit{AP}＝\mathit{AQ}$时，求证： $△\mathit{BPE}≌△\mathit{CQE}$；

（2）如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；并求当 $\mathit{BP}＝2$， $\mathit{CQ}＝9$时BC的长．

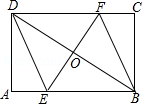
如图，矩形ABCD中，AB＝6，BC＝4，过对角线BD中点O的直线分别交AB，CD边于点E，F．

（1）求证：四边形BEDF是平行四边形；

（2）当四边形BEDF是菱形时，求EF的长．

在数学课本上，同学们已经探究过“经过已知直线外一点作这条直线的垂线“的尺规作图过程：

已知：直线l和l外一点P．

求作：直线l的垂线，使它经过点P．

作法：如图：（1）在直线l上任取两点A、B；

（2）分别以点A、B为圆心，AP，BP长为半径画弧，两弧相交于点Q；

（3）作直线PQ．

参考以上材料作图的方法，解决以下问题：

（1）以上材料作图的依据是：　　

（2）已知，直线l和l外一点P，

求作：⊙P，使它与直线l相切．（尺规作图，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔描黑）

如图1，在平面直角坐标系中，抛物线 y＝ $\frac{\sqrt{3}}{8}$ x ²+ $\frac{3\sqrt{3}}{4}$ x﹣ $\frac{7\sqrt{3}}{8}$ 与 x轴交于点 A、 B（点 A在点 B右侧），点 D为抛物线的顶点，点 C在 y轴的正半轴上， CD交 x轴于点 F，△ CAD绕点 C顺时针旋转得到△ CFE，点 A恰好旋转到点 F，连接 BE．

（1）求点 A、 B、 D的坐标；

（2）求证：四边形 BFCE是平行四边形；

（3）如图2，过顶点 D作 DD ₁⊥ x轴于点 D ₁，点 P是抛物线上一动点，过点 P作 PM⊥ x轴，点 M为垂足，使得△ PAM与△ DD ₁ A相似（不含全等）．

①求出一个满足以上条件的点 P的横坐标；

②直接回答这样的点 P共有几个？

在如图所示的网格中，每个小正方形的边长为1，每个小正方形的顶点叫格点，△ ABC的三个顶点均在格点上，以点 A为圆心的 与 BC相切于点 D，分别交 AB、 AC于点 E、 F．

（1）求△ ABC三边的长；

（2）求图中由线段 EB、 BC、 CF及 所围成的阴影部分的面积．

如图，等边△ ABC中， AB＝6，点 D在 BC上， BD＝4，点 E为边 AC上一动点（不与点 C重合），△ CDE关于 DE的轴对称图形为△ FDE．

（1）当点 F在 AC上时，求证： DF∥ AB；

（2）设△ ACD的面积为 S ₁，△ ABF的面积为 S ₂，记 S＝ S ₁﹣ S ₂， S是否存在最大值？若存在，求出 S的最大值；若不存在，请说明理由；

（3）当 B， F， E三点共线时．求 AE的长．

如图， D是 AB上一点， DF交 AC于点 E， DE＝ FE， FC∥ AB，求证：△ ADE≌△ CFE．

已知Rt△ OAB，∠ OAB＝90°，∠ ABO＝30°，斜边 OB＝4，将Rt△ OAB绕点 O顺时针旋转60°，如图1，连接 BC．

（1）填空：∠ OBC＝ 　　°；

（2）如图1，连接 AC，作 OP⊥ AC，垂足为 P，求 OP的长度；

（3）如图2，点 M， N同时从点 O出发，在△ OCB边上运动， M沿 O→ C→ B路径匀速运动， N沿 O→ B→ C路径匀速运动，当两点相遇时运动停止，已知点 M的运动速度为1.5单位/秒，点 N的运动速度为1单位/秒，设运动时间为 x秒，△ OMN的面积为 y，求当 x为何值时 y取得最大值？最大值为多少？

如图，四边形 ABCD中， AB＝ AD＝ CD，以 AB为直径的⊙ O经过点 C，连接 AC、 OD交于点 E．

（1）证明： OD∥ BC；

（2）若tan∠ ABC＝2，证明： DA与⊙ O相切；

（3）在（2）条件下，连接 BD交⊙ O于点 F，连接 EF，若 BC＝1，求 EF的长．