在数学课本上,同学们已经探究过“经过已知直线外一点作这条直线的垂线“的尺规作图过程:
已知:直线l和l外一点P.
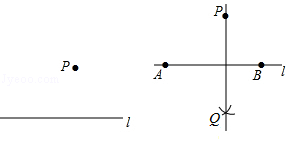
求作:直线l的垂线,使它经过点P.
作法:如图:(1)在直线l上任取两点A、B;
(2)分别以点A、B为圆心,AP,BP长为半径画弧,两弧相交于点Q;
(3)作直线PQ.
参考以上材料作图的方法,解决以下问题:
(1)以上材料作图的依据是:
(2)已知,直线l和l外一点P,
求作:⊙P,使它与直线l相切.(尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
相关知识点
推荐套卷
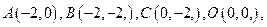 把正方形沿OP对折,使点A落在对角线OB上的E处,折痕交AB于P,试求△EPO的面积。
把正方形沿OP对折,使点A落在对角线OB上的E处,折痕交AB于P,试求△EPO的面积。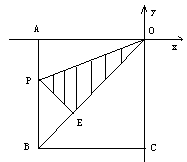
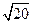 厘米、
厘米、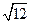 厘米、
厘米、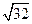 厘米,求三角乡的周长和面积。
厘米,求三角乡的周长和面积。
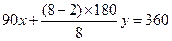 ,整理得:
,整理得: ,
,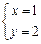 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号