如图1,在 中, , 是 的角平分线,以 为圆心, 为半径作圆交 于点 .
(1)求证:直线 是 的切线;
(2)在图2中,设 与 相切于点 ,连接 ,点 是 的劣弧 上一点,过点 作 的切线,交 于点 ,交 于点 ,已知 的周长为4, ,求 的长.

如图,四边形 是平行四边形,延长 至 ,延长 至 ,使得 ,连接 交 于 ,交 于 .求证: .

如图,在矩形 中,点 在边 上,且 ,过点 作 ,垂足为点
(1)求证: ;
(2)以 为圆心, 长为半径作圆弧交 于点 ,若 ,求扇形 的面积.(结果保留
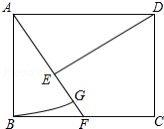
问题引入:
(1)如图①,在 中,点 是 和 平分线的交点,若 ,则 (用 表示);如图②, , , ,则 (用 表示)
拓展研究:
(2)如图③, , , ,请猜想 (用 表示),并说明理由.
类比研究:
(3) 、 分别是 的外角 、 的 等分线,它们交于点 , , , ,请猜想 .
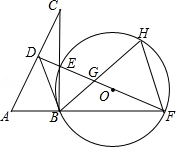
如图,在 中, , 的垂直平分线分别与 , 及 的延长线相交于点 , , , 是 的外接圆, 的平分线交 于点 ,交 于点 ,连接 、 .
(1)试判断 与 的位置关系,并说明理由;
(2)当 时,求 的面积;
(3)在(2)的条件下,求 的值.
如图所示, 中, 是 边上一点, 是 的中点,过点 作 的平行线交 的延长线于 ,且 ,连接 .
(1)求证: 是 的中点;
(2)若 ,试判断四边形 的形状,并证明你的结论.

如图,在 中, , 的平分线交 于点 , ,以点 为圆心 为半径作半圆.
(1)求证: 为 的切线;
(2)如果 ,求 的值.

如图, 为 直径, 为 上一点,点 是 的中点, 于 , 于 .
(1)判断 与 的位置关系,并证明你的结论;
(2)若 ,求 的长度.

阅读下列材料并回答问题:
材料1:如果一个三角形的三边长分别为 , , ,记 ,那么三角形的面积为 . ①
古希腊几何学家海伦 ,约公元50年),在数学史上以解决几何测量问题而闻名.他在《度量》一书中,给出了公式①和它的证明,这一公式称海伦公式.
我国南宋数学家秦九韶(约 约 ,曾提出利用三角形的三边求面积的秦九韶公式: . ②
下面我们对公式②进行变形: .
这说明海伦公式与秦九韶公式实质上是同一公式,所以我们也称①为海伦 秦九韶公式.
问题:如图,在 中, , , , 内切于 ,切点分别是 、 、 .
(1)求 的面积;
(2)求 的半径.

如图, 的对角线 、 交于点 , 过点 且与 、 分别交于点 、 .试猜想线段 、 的关系,并说明理由.

如图,在 中, ,以 边为直径作 交 边于点 ,过点 作 于点 , 、 的延长线交于点 .
(1)求证: 是 的切线;
(2)若 ,且 ,求 的半径与线段 的长.
