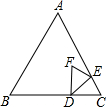
如图，等边△ ABC中， AB＝6，点 D在 BC上， BD＝4，点 E为边 AC上一动点（不与点 C重合），△ CDE关于 DE的轴对称图形为△ FDE．
（1）当点 F在 AC上时，求证： DF∥ AB；
（2）设△ ACD的面积为 S 1，△ ABF的面积为 S 2，记 S＝ S 1﹣ S 2， S是否存在最大值？若存在，求出 S的最大值；若不存在，请说明理由；
（3）当 B， F， E三点共线时．求 AE的长．
）×1.25×（－8）；相关知识点
推荐套卷
如图，等边△ ABC中， AB＝6，点 D在 BC上， BD＝4，点 E为边 AC上一动点（不与点 C重合），△ CDE关于 DE的轴对称图形为△ FDE．
（1）当点 F在 AC上时，求证： DF∥ AB；
（2）设△ ACD的面积为 S 1，△ ABF的面积为 S 2，记 S＝ S 1﹣ S 2， S是否存在最大值？若存在，求出 S的最大值；若不存在，请说明理由；
（3）当 B， F， E三点共线时．求 AE的长．
粤公网安备 44130202000953号