中, , ,点 为直线 上一动点(点 不与 , 重合),以 为边在 右侧作正方形 ,连接 .
(1)观察猜想
如图1,当点 在线段 上时,
① 与 的位置关系为: .
② , , 之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点 在线段 的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
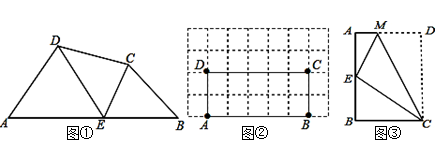
如图3,当点 在线段 的延长线上时,延长 交 于点 ,连接 .若已知 , ,请求出 的长.

相关知识点
推荐套卷
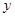 与售出的土豆千克数
与售出的土豆千克数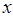 的关系如图所示,结合图象回答下列问题.
的关系如图所示,结合图象回答下列问题.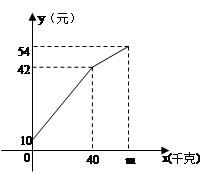

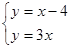
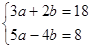
 粤公网安备 44130202000953号
粤公网安备 44130202000953号