某学校九年级的学生去旅游,在风景区看到一棵古松,不知这棵古松有多高,下面是他们的一段对话:
甲:我站在此处看树顶仰角为45°。
乙:我站在此处看树顶仰角为30°。
甲:我们的身高都是1.5m。
乙:我们相距20m。
请你根据两位同学的对话,参考图7计算这棵古松的高度。(参考数据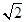 ≈1.414,
≈1.414,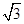 ≈1
≈1 .732,结果保留两位小数)。
.732,结果保留两位小数)。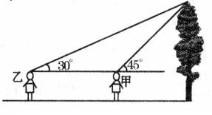
相关知识点
推荐套卷
某学校九年级的学生去旅游,在风景区看到一棵古松,不知这棵古松有多高,下面是他们的一段对话:
甲:我站在此处看树顶仰角为45°。
乙:我站在此处看树顶仰角为30°。
甲:我们的身高都是1.5m。
乙:我们相距20m。
请你根据两位同学的对话,参考图7计算这棵古松的高度。(参考数据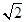 ≈1.414,
≈1.414,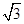 ≈1
≈1 .732,结果保留两位小数)。
.732,结果保留两位小数)。