如图①， 中， ， 于点 ，点 在 上，且 ，连接 ．
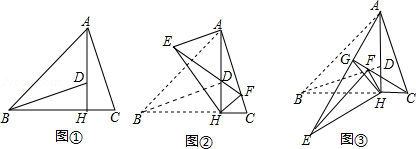
（1）求证： ；
（2）将 绕点 旋转，得到 （点 ， 分别与点 ， 对应），连接 ．
①如图②，当点 落在 上时， 不与 重合），若 ， ，求 的长；
②如图③，当 是由 绕点 逆时针旋转 得到时，设射线 与 相交于点 ，连接 ，试探究线段 与 之间满足的等量关系，并说明理由．
（成都）（本小题满分10分）如图，在Rt△ABC中，∠ABC=90°，AC的垂直平分线分别与AC，BC及AB的延长线相交于点D，E，F，且BF=BC．⊙O是△BEF的外接圆，∠EBF的平分线交EF于点G，交于点H，连接BD、FH．
（1）求证：△ABC≌△EBF；
（2）试判断BD与⊙O的位置关系，并说明理由；
（3）若AB=1，求HG•HB的值．
（成都）（本小题满分10分）已知AC，EC分别为四边形ABCD和EFCG的对角线，点E在△ABC内，∠CAE+∠CBE=90．
（1）如图①，当四边形ABCD和EFCG均为正方形时，连接BF．
i）求证：△CAE∽△CBF；
ii）若BE=1，AE=2，求CE的长；
（2）如图②，当四边形ABCD和EFCG均为矩形，且
时，若BE＝1，AE=2，CE=3，求k的值；
（3）如图③，当四边形ABCD和EFCG均为菱形，且∠DAB=∠GEF=45°时，设BE=m，AE=n，CE=p，试探究m，n，p三者之间满足的等量关系．（直接写出结果，不必写出解答过程）
（成都）（本小题满分12分）如图，在平面直角坐标系xOy中，抛物线
（
）与x轴交于A，B两点（点A在点B的左侧），经过点A的直线l：
与y轴负半轴交于点C，与抛物线的另一个交点为D，且CD=4AC．
（1）直接写出点A的坐标，并求直线l的函数表达式（其中k，b用含a的式子表示）；
（2）点E是直线l上方的抛物线上的动点，若△ACE的面积的最大值为
，求a的值；
（3）设P是抛物线的对称轴上的一点，点Q在抛物线上，以点A，D，P，Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由．
（乐山）“六一”期间，小张购进100只两种型号的文具进行销售，其进价和售价之间的关系如下表：
（1）小张如何进货，使进货款恰好为1300元？
（2）要使销售文具所获利润最大，且所获利润不超过进货价格的40%，请你帮小张设计一个进货方案，并求出其所获利润的最大值．
粤公网安备 44130202000953号