(本小题满分10 分)已知 (
( )的展开式中
)的展开式中 的系数为11.
的系数为11.
(1)求 的系数的最小值;
的系数的最小值;
(2)当 的系数取得最小值时,求
的系数取得最小值时,求 展开式中
展开式中 的奇次幂项的系数之和.
的奇次幂项的系数之和.
(本小题满分14分)在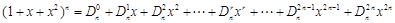 的展开式中,把
的展开式中,把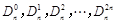 叫做三项式系数.
叫做三项式系数.
(Ⅰ)当 时,写出三项式系数
时,写出三项式系数 的值;
的值;
(Ⅱ)二项式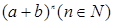 的展开式中,系数可用杨辉三角形数阵表示,如图:
的展开式中,系数可用杨辉三角形数阵表示,如图:
当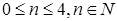 时,类似杨辉三角形数阵表,请列出三项式的
时,类似杨辉三角形数阵表,请列出三项式的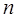 次系数列的数阵表;
次系数列的数阵表;
(Ⅲ)求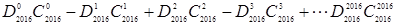 的值(可用组合数作答).
的值(可用组合数作答).
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
| 零件的个数x |
3 |
4 |
5 |
6 |
| 加工的时间y |
2.5 |
3 |
4 |
4.5 |
据相关性检验,这组样本数据具有线性相关关系,通过线性回归分析,求得其回归直线的斜率为0.7,则这组样本数据的回归直线方程是( )
A.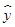 =0.7x+0.35 B.
=0.7x+0.35 B.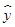 =0.7x+1
=0.7x+1
C.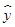 =0.7x+2.05 D.
=0.7x+2.05 D.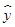 =0.7x+0.45
=0.7x+0.45
(本小题满分13分)已知抛物线 的焦点
的焦点 以及椭圆
以及椭圆 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆 上.
上.
(1)求抛物线 和椭圆
和椭圆 的标准方程;
的标准方程;
(2)过点 的直线交抛物线
的直线交抛物线 于
于 、
、 两不同点,交
两不同点,交 轴于点
轴于点 ,已知
,已知 为定值.
为定值.
(本小题满分13分)已知椭圆 的离心率
的离心率 ,直线
,直线 与椭圆交于
与椭圆交于 两点,
两点, 为椭圆的右顶点,
为椭圆的右顶点, 
(1)求椭圆的方程;
(2)若椭圆上存在两点 使
使 ,求
,求 面积的最大值.
面积的最大值.
(本题满分12分,第(1)小题5分,第(2)小题7分)
如图, 是圆柱体
是圆柱体 的一条母线,已知
的一条母线,已知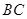 过底面圆的圆心
过底面圆的圆心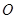 ,
, 是圆
是圆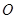 上不与点
上不与点 重合的任意一点,
重合的任意一点, ,
, ,
, .
.
(1)求直线 与直线
与直线 所成角的大小;
所成角的大小;
(2)将四面体 绕母线
绕母线 旋转一周,求
旋转一周,求 的三边在旋转过程中所围成的几何体的体积.
的三边在旋转过程中所围成的几何体的体积.
(本题满分18分,第(1)小题4分,第(2)小题5分,第(3)小题9分)
设函数 的定义域为
的定义域为 ,值域为
,值域为 ,如果存在函数
,如果存在函数 ,使得函数
,使得函数 的值域仍是
的值域仍是 ,那么称
,那么称 是函数
是函数 的一个等值域变换.
的一个等值域变换.
(1)判断下列函数 是不是函数
是不是函数 的一个等值域变换?说明你的理由;
的一个等值域变换?说明你的理由; ,
, ;
; ,
, .
.
(2)设函数 的定义域为
的定义域为 ,值域为
,值域为 ,函数
,函数 的定义域为
的定义域为 ,值域为
,值域为 ,那么“
,那么“ ”是否为“
”是否为“ 是
是 的一个等值域变换”的一个必要条件?请说明理由;
的一个等值域变换”的一个必要条件?请说明理由;
(3)设 的定义域为
的定义域为 ,已知
,已知 是
是 的一个等值域变换,且函数
的一个等值域变换,且函数 的定义域为
的定义域为 ,求实数
,求实数 的值.
的值.
(本题满分13分,第(1)小题5分,第(2)小题8分)
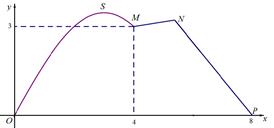
如图所示,某市拟在长为 道路
道路 的一侧修建一条运动赛道,赛道的前一部分为曲线段
的一侧修建一条运动赛道,赛道的前一部分为曲线段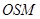 ,该曲线段为函数
,该曲线段为函数
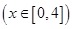 的图像,且图像的最高点为
的图像,且图像的最高点为 ,赛道的后一部分为折线段
,赛道的后一部分为折线段 ,且
,且 .
.
(1)求 、
、 两点间的直线距离;
两点间的直线距离;
(2)求折线段赛道 长度的最大值.
长度的最大值.
(本小题满分14分)已知椭圆 的离心率
的离心率 ,它的一
,它的一
个顶点在抛物线 的准线上.
的准线上.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设 是椭圆
是椭圆 上两点,已知
上两点,已知 ,且
,且 .
.
(ⅰ)求 的取值范围;
的取值范围;
(ⅱ)判断 的面积是否为定值?若是,求出该定值,不是请说明理由.
的面积是否为定值?若是,求出该定值,不是请说明理由.
己知函数 .
.
(Ⅰ)若 x =  为 f (x)的极值点, 求实数a的值;
为 f (x)的极值点, 求实数a的值;
(Ⅱ)若 y =" f" (x)在[l, +∞)上为增函数, 求实数a的取值范围;
(Ⅲ)若a=-1时, 方程  有实根, 求实数b的取值范围.
有实根, 求实数b的取值范围.
已知F1F2是椭圆 =" 1" (a > b > 0)的两个焦点, O为坐标原点, 点 P(-1,
=" 1" (a > b > 0)的两个焦点, O为坐标原点, 点 P(-1, )在椭圆
)在椭圆
上, 且 是以F1F2为直径的圆, 直线
是以F1F2为直径的圆, 直线 : y=kx+m与⊙O相切, 并且与椭圆交于
: y=kx+m与⊙O相切, 并且与椭圆交于
不同的两点A、 B.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)当  , 且满足
, 且满足 时, 求弦长|AB|的取值范围.
时, 求弦长|AB|的取值范围.
已知F1F2是椭圆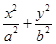 =" 1" (a > b > 0)的两个焦点, O为坐标原点, 点 P(-1,
=" 1" (a > b > 0)的两个焦点, O为坐标原点, 点 P(-1, )在椭圆上, 且
)在椭圆上, 且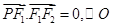 是以F1F2为直径的圆, 直线
是以F1F2为直径的圆, 直线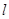 : y=kx+m与⊙O相切, 并且与椭圆交于不同的两点A、 B.
: y=kx+m与⊙O相切, 并且与椭圆交于不同的两点A、 B.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)当 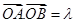 , 且满足
, 且满足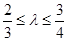 时, 求弦长|AB|的取值范围.
时, 求弦长|AB|的取值范围.