辽宁省锦州市高三质量检测二理科数学试卷
已知全集U=R, 集合A=  , 则{ x|x≤0 }等于
, 则{ x|x≤0 }等于
(A)A∩B (B)A∪B (C)∁U(A∩B)(D)∁U(A∪B)
下列说法不正确的是
| A.若“p且q”为假,则p、 q至少有一个是假命题 |
B.命题“∃x0∈R,x -x0-<0”的否定是“∀x∈R,x2-x-1≥0” -x0-<0”的否定是“∀x∈R,x2-x-1≥0” |
C.“ ”是“y="sin" (2x+ ”是“y="sin" (2x+ )为偶函数”的充要条件 )为偶函数”的充要条件 |
| D.α<0时,幂函数y=xa在 (0, +∞)上单调递减 |
某几何体的三视图如下图所示, 则该几何体的体积为
| A.200+9π |
| B.200+18π |
| C.140+9π |
| D.140+18π |
已知x、 y满足约束条件 则 z =" x" + 2y 的最大值为
则 z =" x" + 2y 的最大值为
| A.-2 | B.-1 | C.1 | D.2 |
若如图所示的程序框图输出的S是30, 则在判断框中M表示的 “条件” 应该是
| A.n≥3 | B.n≥4 | C.n≥5 | D.n≥6 |
已知向量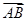 与
与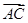 的夹角为120°, 且 |
的夹角为120°, 且 |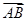 | = 2, |
| = 2, |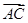 | = 3,若
| = 3,若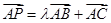 且
且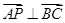 ,则实数λ的值为
,则实数λ的值为
A.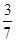 |
B.13 | C.6 | D.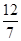 |
分配4名水暖工去3个不同的居民家里检查暖气管道, 要求4名水暖工都分配出去, 并每
名水暖工只去一个居民家, 且每个居民家都要有人去检查, 那么分配的方案共有
A. 种 种 |
B. 种 种 |
C. 种 种 |
D. 种 种 |
函数 f (x)=" sin(2x" + 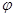 )( |
)( |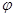 | <
| < 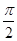 )的图象向左平移
)的图象向左平移 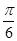 个单位后关于原点对称, 则函数 f (x)在[0,
个单位后关于原点对称, 则函数 f (x)在[0, 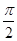 ]上的最小值为
]上的最小值为
A.-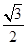 |
B.-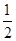 |
C.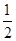 |
D.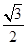 |
过双曲线 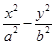 =" 1" (a > 0,b > 0)的一个焦点F向其一条渐近线作垂线
=" 1" (a > 0,b > 0)的一个焦点F向其一条渐近线作垂线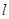 , 垂足为A,
, 垂足为A,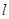 与另一条渐近线交于B点, 若
与另一条渐近线交于B点, 若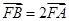 , 则双曲线的离心率为
, 则双曲线的离心率为
| A.2 | B.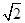 |
C.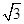 |
D.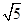 |
设函数 f (x)的导函数为 f ′(x), 对任意x∈R都有 f (x)> f′(x)成立, 则
| A.3f(ln2)<2f(ln3) |
| B.3f(ln2)=2f(ln3) |
| C.3f(ln2)>2f(ln3) |
| D.3f(ln2)与2f(ln3)的大小不确定 |
设函数 f (x)="(x" + a)n, 其中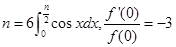 , 则 f (x)的展开式中的x4系数为______.
, 则 f (x)的展开式中的x4系数为______.
已知抛物线C:y2=" 2px" (p > 0)的焦点为F, 过点F倾斜角为60°的直线l与抛物线C在第一、 四象限分别交于A、 B两点, 则 的值等于_____________.
的值等于_____________.
已知数列{an}的前n项和为Sn, 且满足a1 = 2, nan + 1 = Sn + n(n + 1).
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)设Tn为数列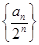 }的前n项和, 求Tn;
}的前n项和, 求Tn;
(Ⅲ)设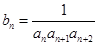 , 证明:
, 证明: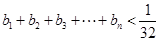
如图, 在直三棱柱 ABC - A1B1C1中, D、 E分别是BC和CC1的中点, 已知AB=AC=AA1=4,∠BAC=90°.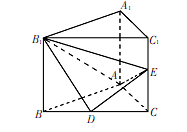
(Ⅰ)求证: B1D⊥平面AED;
(Ⅱ)求二面角B1-AE-D的余弦值;
(Ⅲ)求三棱锥A-B1DE的体积.
心理学家分析发现视觉和空间能力与性别有关, 某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学 (男30女20), 给所有同学几何题和代数题各一题, 让各位同学自由选择一道题进行解答.选题情况如下表:(单位: 人)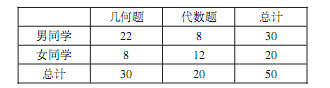
(Ⅰ)能否据此判断有97.5%的把握认为视觉和空间能力与性别有关?
(Ⅱ)经过多次测试后, 甲每次解答一道几何题所用的时间在5—7分钟, 乙每次解答一道几何题所用的时间在6—8分钟, 现甲、 乙各解同一道几何题, 求乙比甲先解答完的概率.
(Ⅲ)现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、 乙两女生被抽到的人数为X, 求X的分布列及数学期望E (X).
附表及公式
已知F1F2是椭圆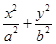 =" 1" (a > b > 0)的两个焦点, O为坐标原点, 点 P(-1,
=" 1" (a > b > 0)的两个焦点, O为坐标原点, 点 P(-1, )在椭圆上, 且
)在椭圆上, 且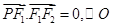 是以F1F2为直径的圆, 直线
是以F1F2为直径的圆, 直线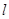 : y=kx+m与⊙O相切, 并且与椭圆交于不同的两点A、 B.
: y=kx+m与⊙O相切, 并且与椭圆交于不同的两点A、 B.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)当 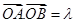 , 且满足
, 且满足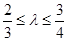 时, 求弦长|AB|的取值范围.
时, 求弦长|AB|的取值范围.
己知函数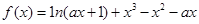 .
.
(Ⅰ)若 x = 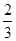 为 f (x)的极值点, 求实数a的值;
为 f (x)的极值点, 求实数a的值;
(Ⅱ)若 y =" f" (x)在[l, +∞)上为增函数, 求实数a的取值范围;
(Ⅲ)若a=-1时, 方程 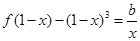 有实根, 求实数b的取值范围
有实根, 求实数b的取值范围
选修4-1: 几何证明选讲.
如图, 圆M与圆N交于A, B两点, 以A为切点作两圆的切线分别交圆M和圆N于C, D
两点,延长DB交圆M于点E, 延长CB交圆N于点F.已知BC=5, DB=10.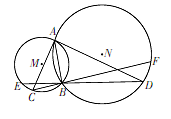
(Ⅰ)求AB的长;
(Ⅱ)求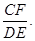
选修4-4: 坐标系与参数方程
在极坐标系中, 已知圆C的圆心C( ), 半径r =
), 半径r =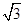 .
.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)若 α ∈ 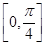 , 直线
, 直线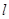 的参数方程为
的参数方程为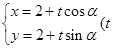 为参数), 直线
为参数), 直线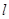 交圆C于A、 B两点, 求弦长|AB|的取值范围.
交圆C于A、 B两点, 求弦长|AB|的取值范围.
 , 则z等于
, 则z等于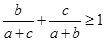 , 则角A的范围是
, 则角A的范围是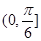
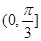
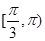
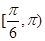
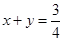 , 则
, 则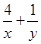 的最小值为____________.
的最小值为____________.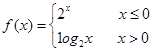 , 且函数
, 且函数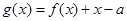 只有一个零点, 则实数a的取值范围是_____________.
只有一个零点, 则实数a的取值范围是_____________. 粤公网安备 44130202000953号
粤公网安备 44130202000953号