上海市闸北区高三下学期期中练习(二模)理科数学试卷
设复数 ,在复平面的对应的向量分别为
,在复平面的对应的向量分别为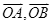 ,则向量
,则向量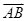 对应的复数所对应的点的坐标为____________.
对应的复数所对应的点的坐标为____________.
一个篮球运动员投篮一次得3分的概率为 ,得2分的概率为
,得2分的概率为 ,不得分的概率为
,不得分的概率为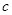 ,其中
,其中 .已知投篮一次得分的期望是2,则
.已知投篮一次得分的期望是2,则 的最大值是____________.
的最大值是____________.
若二项式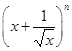 展开式中只有第四项的系数最大,则这个展开式中任取一项为有理项的概率是____________.
展开式中只有第四项的系数最大,则这个展开式中任取一项为有理项的概率是____________.
从双曲线 的左焦点
的左焦点 引圆
引圆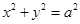 的切线,切点为
的切线,切点为 ,延长
,延长 交双曲线右支于点
交双曲线右支于点 ,若
,若 是线段
是线段 的中点,
的中点, 为坐标原点,则
为坐标原点,则 的值是____________.
的值是____________.
已知集合 ,
,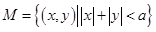 ,
, ,现给出下列函数:①
,现给出下列函数:① ;②
;②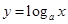 ;③
;③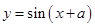 ;④
;④ .若
.若 时,恒有
时,恒有 ,则所有满足条件的函数
,则所有满足条件的函数 的编号是___________.
的编号是___________.
把正整数排列成如图 的三角形数阵,然后擦去第偶数行中的所有奇数、第奇数行中的所有偶数,可得到如图
的三角形数阵,然后擦去第偶数行中的所有奇数、第奇数行中的所有偶数,可得到如图 的三角形数阵,现将图
的三角形数阵,现将图 中的正整数按从小到大的顺序构成一个数列
中的正整数按从小到大的顺序构成一个数列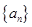 ,若
,若 ,则
,则

下列命题中,正确的个数是
(1)直线上有两个点到平面的距离相等,则这条直线和这个平面平行;
(2) 、
、 为异面直线,则过
为异面直线,则过 且与
且与 平行的平面有且仅有一个;
平行的平面有且仅有一个;
(3)直四棱柱是直平行六面体;
(4)两相邻侧面所成角相等的棱锥是正棱锥.
| A.0 | B.1 | C.2 | D.3 |
在极坐标系中,关于曲线 的下列判断中正确的是
的下列判断中正确的是
A.曲线 关于直线 关于直线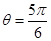 对称 对称 |
B.曲线 关于直线 关于直线 对称 对称 |
C.曲线 关于点 关于点 对称 对称 |
D.曲线 关于极点 关于极点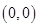 对称 对称 |
(本题满分12分,第(1)小题5分,第(2)小题7分)
如图,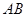 是圆柱体
是圆柱体 的一条母线,已知
的一条母线,已知 过底面圆的圆心
过底面圆的圆心 ,
, 是圆
是圆 上不与点
上不与点 重合的任意一点,
重合的任意一点,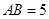 ,
, ,
, .
.
(1)求直线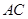 与平面
与平面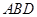 所成角的大小;
所成角的大小;
(2)将四面体 绕母线
绕母线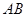 旋转一周,求
旋转一周,求 的三边在旋转过程中所围成的几何体的体积.
的三边在旋转过程中所围成的几何体的体积.
(本题满分13分,第(1)小题5分,第(2)小题8分)
如图所示,某市拟在长为 道路
道路 的一侧修建一条运动赛道,赛道的前一部分为曲线段
的一侧修建一条运动赛道,赛道的前一部分为曲线段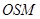 ,该曲线段为函数
,该曲线段为函数
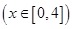 的图像,且图像的最高点为
的图像,且图像的最高点为 ,赛道的后一部分为折线段
,赛道的后一部分为折线段 ,且
,且 .
.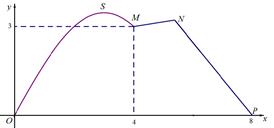
(1)求 、
、 两点间的直线距离;
两点间的直线距离;
(2)求折线段赛道 长度的最大值.
长度的最大值.
(本题满分14分,第(1)小题5分,第(2)小题9分)
已知圆 ,点
,点 ,点
,点 在圆
在圆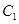 上运动,
上运动,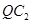 的垂直平分线交
的垂直平分线交 于点
于点 .
.
(1)求动点 的轨迹
的轨迹 方程;
方程;
(2)过点 且斜率为
且斜率为 的动直线
的动直线 交曲线
交曲线 于
于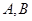 两点,在
两点,在 轴上是否存在定点
轴上是否存在定点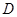 ,使以
,使以 为直径的圆恒过这个点?若存在,请求出点
为直径的圆恒过这个点?若存在,请求出点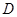 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(本题满分18分,第(1)小题4分,第(2)小题5分,第(3)小题9分)
设函数 的定义域为
的定义域为 ,值域为
,值域为 ,如果存在函数
,如果存在函数 ,使得函数
,使得函数 的值域仍是
的值域仍是 ,那么称
,那么称 是函数
是函数 的一个等值域变换.
的一个等值域变换.
(1)判断下列函数 是不是函数
是不是函数 的一个等值域变换?说明你的理由;
的一个等值域变换?说明你的理由; ,
, ;
; ,
, .
.
(2)设函数 的定义域为
的定义域为 ,值域为
,值域为 ,函数
,函数 的定义域为
的定义域为 ,值域为
,值域为 ,那么“
,那么“ ”是否为“
”是否为“ 是
是 的一个等值域变换”的一个必要条件?请说明理由;
的一个等值域变换”的一个必要条件?请说明理由;
(3)设 的定义域为
的定义域为 ,已知
,已知 是
是 的一个等值域变换,且函数
的一个等值域变换,且函数 的定义域为
的定义域为 ,求实数
,求实数 的值.
的值.
 的图像经过点
的图像经过点 ,则函数
,则函数 的函数
的函数 的图像关于点
的图像关于点 对称,
对称, 是
是 ,则
,则 ___________.
___________. 数列
数列 的前
的前 项和为
项和为 ,则
,则 ___________.
___________. ,若存在互不相等的实数
,若存在互不相等的实数 满足
满足 ,则
,则 的取值范围是_____________.
的取值范围是_____________. 是正三角形
是正三角形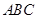 内部的一点,
内部的一点, ,则
,则 的面积与
的面积与 的面积之比是
的面积之比是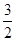
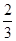


 按次序排成一列,称之为向量列,记作
按次序排成一列,称之为向量列,记作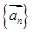 ,已知向量列
,已知向量列 ,
,
 .
. 是等比数列;
是等比数列; ,问数列
,问数列 中是否存在最小项?若存在,求出最小项;若不存在,请说明理由;
中是否存在最小项?若存在,求出最小项;若不存在,请说明理由; 表示向量
表示向量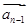 与
与 间的夹角,若
间的夹角,若 ,对于任意正整数
,对于任意正整数 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的范围.
的范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号