(本题满分18分,第(1)小题4分,第(2)小题5分,第(3)小题9分)
设函数 的定义域为
的定义域为 ,值域为
,值域为 ,如果存在函数
,如果存在函数 ,使得函数
,使得函数 的值域仍是
的值域仍是 ,那么称
,那么称 是函数
是函数 的一个等值域变换.
的一个等值域变换.
(1)判断下列函数 是不是函数
是不是函数 的一个等值域变换?说明你的理由;
的一个等值域变换?说明你的理由; ,
, ;
; ,
, .
.
(2)设函数 的定义域为
的定义域为 ,值域为
,值域为 ,函数
,函数 的定义域为
的定义域为 ,值域为
,值域为 ,那么“
,那么“ ”是否为“
”是否为“ 是
是 的一个等值域变换”的一个必要条件?请说明理由;
的一个等值域变换”的一个必要条件?请说明理由;
(3)设 的定义域为
的定义域为 ,已知
,已知 是
是 的一个等值域变换,且函数
的一个等值域变换,且函数 的定义域为
的定义域为 ,求实数
,求实数 的值.
的值.
相关知识点
推荐套卷

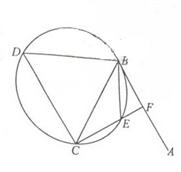
 ,延长CE交AB于点F,求△BCF外接圆的半径。
,延长CE交AB于点F,求△BCF外接圆的半径。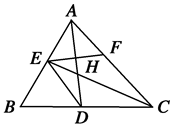
 粤公网安备 44130202000953号
粤公网安备 44130202000953号