如图是导函数 的图象:
的图象:
① 处导函数
处导函数 有极大值;
有极大值;
②在 处导函数
处导函数 有极小值;
有极小值;
③在 处函数
处函数 有极大值;
有极大值;
④在 处函数
处函数 有极小值;以上叙述正确的是____________。
有极小值;以上叙述正确的是____________。
(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系 中,以原点O为极点,
中,以原点O为极点, 轴的正半轴为极轴,建立极坐标系,已知圆C的极坐标方程为
轴的正半轴为极轴,建立极坐标系,已知圆C的极坐标方程为
 。
。
(Ⅰ)当 时,设
时,设 为圆C的直径,求点
为圆C的直径,求点 的极坐标;
的极坐标;
(Ⅱ)直线 的参数方程是
的参数方程是 (
( 为参数),直线
为参数),直线 被圆C截得的弦长为
被圆C截得的弦长为 ,若
,若 ,求
,求 的取值范围。
的取值范围。
(本小题满分12分) 已知函数 .
.
(1)当 时,求函数
时,求函数 的单调区间和极值;;
的单调区间和极值;;
(2) 若 恒成立,求实数
恒成立,求实数 的值。
的值。
(本小题满分12分)某商区停车场临时停车按时段收费,收费标准为:每辆汽车一次停车不超过 小时收费
小时收费 元,超过
元,超过 小时的部分每小时收费
小时的部分每小时收费 元(不足
元(不足 小时的部分按
小时的部分按 小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过
小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过 小时.
小时.
(1)若甲停车 小时以上且不超过
小时以上且不超过 小时的概率为
小时的概率为 ,停车付费多于
,停车付费多于 元的概率为
元的概率为 ,求甲停车付费恰为
,求甲停车付费恰为 元的概率;
元的概率;
(2)若每人停车的时长在每个时段的可能性相同,求甲、乙二人停车付费之和为 元的概率.
元的概率.
已知函数f(x)的定义域为[-1,5],部分对应值如下表.
| x |
-1 |
0 |
4 |
5 |
| f(x) |
1 |
2 |
2 |
1 |
f(x)的导函数y=f′(x)的图象如图所示.下列关于函数f(x)的命题: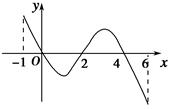
①函数y=f(x)是周期函数;
②函数f(x)在[0,2]是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)-a有4个零点.
其中真命题的个数是 ( )
A.4 B.3 C.2 D.1
(本小题满分13分)设数列 的前
的前 项和为
项和为 ,对一切
,对一切 ,点
,点 都在函数
都在函数 的图象上
的图象上
(1)求 归纳数列
归纳数列 的通项公式(不必证明);
的通项公式(不必证明);
(2)将数列 依次按1项、2项、3项、4项循环地分为(
依次按1项、2项、3项、4项循环地分为( ),
), ,
, ,
,  ;
; ,
, ,
, ,
, ;
; , ..,
, ..,
分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为 ,求
,求 的值;
的值;
(3)设 为数列
为数列 的前
的前 项积,若不等式
项积,若不等式 对一切
对一切  都成立,其中
都成立,其中 ,求
,求 的取值范围
的取值范围
(本小题满分14分)设函数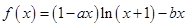 ,其中
,其中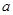 和
和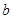 是实数,曲线
是实数,曲线 恒与
恒与 轴相切于坐标原点.
轴相切于坐标原点.
(1)求常数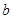 的值;
的值;
(2)当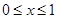 时,关于
时,关于 的不等式
的不等式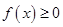 恒成立,求实数
恒成立,求实数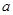 的取值范围;
的取值范围;
(3)求证: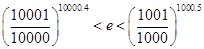 .
.
关于圆周率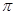 ,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计
,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计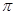 的值:先请120名同学,每人随机写下一个都小于1 的正实数对(x,y);再统计两数能与1构成钝角三角形三边的数对(x,y)的个数m;最后再根据统计数m来估计
的值:先请120名同学,每人随机写下一个都小于1 的正实数对(x,y);再统计两数能与1构成钝角三角形三边的数对(x,y)的个数m;最后再根据统计数m来估计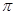 的值.假如统计结果是m=34,那么可以估计
的值.假如统计结果是m=34,那么可以估计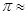 .(用分数表示)
.(用分数表示)
(本题满分12分)
已知函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)设函数 ,若
,若 ,使得
,使得 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(3)若方程 有两个不相等的实数根
有两个不相等的实数根 ,求证:
,求证:
(本小题满分12分)
一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取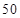 个作为样本,称出它们的重量(单位:克),重量分组区间为
个作为样本,称出它们的重量(单位:克),重量分组区间为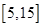 ,
,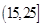 ,
, ,
,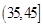 ,由此得到样本的重量频率分布直方图(如下图),
,由此得到样本的重量频率分布直方图(如下图),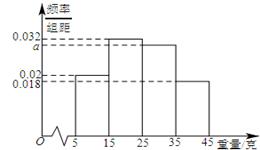
(1)求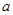 的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;
的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;
(2)从盒子中随机抽取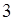 个小球,其中重量在
个小球,其中重量在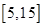 内的小球个数为
内的小球个数为 ,求
,求 的分布列和数学期望. (以直方图中的频率作为概率).
的分布列和数学期望. (以直方图中的频率作为概率).