海南省高三5月模拟文科数学试卷

已知集合，则M∩N=（ ）

A．

B．

C．

D．

复数的共轭复数是（ ）

A．

B．

C．

D．

若满足约束条件：；则的取值范围为 （  ）

A．

B．

C．

D．

已知函数和的图象的对称轴完全相同，若，则的取值范围是（  ）

A．

B．

C．

D．

执行右图所示的程序框图（其中表示不超过x的最大整数），则输出的S值为（  ）

从数字0，1，2，3，4，5中任取两个数组成两位数，其中奇数的概率为（  ）

A．

B．

C．

D．

知图是一个空间几何体的三视图，则该几何体的体积为（    ）

A．	B．
C．	D．

各项都为正数的等比数列的前项和为，若，，则公比的值是        （   ）

A．

B．

C．

D．

设点P是双曲线与圆x²＋y²＝a²＋b²在第一象限的交点，F₁、F₂分别是双曲线的左、右焦点，且|PF₁|＝3|PF₂|，则双曲线的离心率为（ ）

A．

B．

C．

D．

已知函数，其中．若对于任意的，都有，则的取值范围是（   ）

A．

B．

C．

D．

已知函数f（x）的定义域为[－1,5]，部分对应值如下表．

 
f（x）的导函数y＝f′（x）的图象如图所示．下列关于函数f（x）的命题：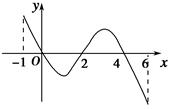

①函数y＝f（x）是周期函数；
②函数f（x）在[0,2]是减函数；
③如果当x∈[－1，t]时，f（x）的最大值是2，那么t的最大值为4；
④当1<a<2时，函数y＝f（x）－a有4个零点．
其中真命题的个数是 （ ）
A．4             B．3             C．2               D．1

在等腰直角△ABC中，点O是斜边BC的中点，过点O的直线分别交直线AB、AC于不同的两点M、N，若，,则的最大值为（  ）
A．3               B．2            C． 1              D．

已知抛物线C的顶点在坐标原点，焦点为F（1,0），过焦点F的直线l与抛物线C相交于A、B两点，若直线l的倾斜角为45°，则弦AB的中点坐标为          

如图，正六边形的边长为，则______

已知函数的图象与y轴的交点为，
它在y轴右侧的第一个最高点和第一个最低点的坐标分别为和则=               

已知两个圆锥有公共底面，且两圆锥的顶点和底面的圆周都在同一个球面上．若圆锥底面面积是这个球面面积的，则这两个圆锥中，体积较小者的高与体积较大者的高的比值为_______

（本小题满分12分）已知数列{a_n}满足：a₁=20，a₂=7，a_n+2﹣a_n=﹣2（n∈N*）．
（Ⅰ）求a₃，a₄，并求数列{a_n}通项公式；
（Ⅱ）记数列{a_n}前2n项和为S_2n，当S_2n取最大值时，求n的值．

（本小题满分12分）某商区停车场临时停车按时段收费，收费标准为：每辆汽车一次停车不超过小时收费元，超过小时的部分每小时收费元（不足小时的部分按小时计算）．现有甲、乙二人在该商区临时停车，两人停车都不超过小时．
（1）若甲停车小时以上且不超过小时的概率为，停车付费多于元的概率为，求甲停车付费恰为元的概率；
（2）若每人停车的时长在每个时段的可能性相同，求甲、乙二人停车付费之和为元的概率．

（本小题满分12分） 在三棱柱中，侧面为矩形，，D为的中点，BD与交于点O，侧面．

（1）证明：；
（2）若，求三棱锥的体积．

（本小题满分12分）已知圆的方程为，过点作圆的两条切线，切点分别为、，直线恰好经过椭圆：的右顶点和上顶点．
（1）求直线的方程及椭圆的方程；
（2）若椭圆以的长轴为短轴,且与有相同的离心率，点A,B分别在椭圆和上,（为原点），求直线的方程．

（本小题满分12分） 已知函数．
（1）当时，求函数的单调区间和极值；；
（2） 若恒成立，求实数的值。

（本小题满分10分）选修41：如图，AB是圆O的直径，C，D是圆O上两点，AC与BD相交于点E，GC，GD是圆O的切线，点F在DG的延长线上，且。求证：

（1）D、E、C、F四点共圆；      
（2）

（本小题满分10分）选修4-4：坐标系与参数方程
在平面直角坐标系中，以原点O为极点，轴的正半轴为极轴，建立极坐标系，已知圆C的极坐标方程为。
（Ⅰ）当时，设为圆C的直径，求点的极坐标；
（Ⅱ）直线的参数方程是（为参数），直线被圆C截得的弦长为，若，求的取值范围。

（本小题满分10分）选修45：已知函数。
（1）解不等式；
（2）若，且，求证：。